S.L. Taylor, M.E. Payton and W.R. Raun*

Contribution from the Okla. Agric. Exp. Sta., Department of Plant and Soil Sciences, 044 North Agricultural Hall, and Department of Statistics, 301 Math Sciences, Oklahoma State University, Stillwater, OK 74078, *Corresponding author.

Large coefficients of variation (>30%) are often associated with increased experimental variability. The objective of this study was to examine the relationships between mean square errors, yield means, coefficients of variation (CV) and plot size using statistical information compiled from past wheat field research projects. Three hundred and sixty two wheat field research projects were selected from over 2000 published wheat experiments that included soil fertility, weed, tillage, and variety evaluation. Little or no relationship between mean square error (MSE) and mean yield or plot size was found. However, mean yields and CVs demonstrated a significant negative correlation. This work proposes decreased variability among experimental units as defined by the CV can be accomplished simply by increasing the mean yield, suggesting that the use of the CV may be improper when comparing variability of trials from similar experiments. Attempts to compare variation from similar experiments should be done using the MSE since unit differences would not be a problem. The CV should only be used when comparing variation from experiments using different metrics. Plot size in plant breeding variety trials (average of 3.59m2) was much smaller than that in fertilizer/weed/tillage trials (average of 37.2m2). The smaller plot size employed in the variety trials reduced the variability encountered in the estimation of the mean and is consistent with the resolution where detectable differences in soil test parameters exist and that should be treated independently.

Experimental error is defined as a measure of the variation which exists among observations on experimental units treated alike (Steel et al. 1997, p. 129). Steel et al., (1997) further noted that variation comes from two main sources; 1) inherent variability that exists in the experimental material to which treatments are applied and 2) variation which results from any lack in uniformity in the physical conduct of the experiment.

Coefficients of variation were first employed as relative measures of variation. The CV is defined as the standard deviation expressed as a percentage of the mean (Tippett, 1952; Senders, 1958; Steel et al. 1997; Lewis, 1963). Mills (1924) indicated that the CV is affected by the value of the mean, as well as by the size of the standard deviation. Since the CV is a ratio, Zar (1984, p. 32) claimed that the CV should only be used for ratio-type data. The CV should not be used for strictly interval or nominal data since ratios have no explicit meaning with these data types.

Conceptually, the CV is not defined for means equal to zero, and the CV is unreliable for means that are close to zero relative to the standard deviation. This often poses problems for researchers who wish to use the CV. However, if the data is truly ratio-type data, this scenario will not occur since small valued means (relative to the standard deviation) cannot occur.

Moore (1958) found that if it is desired to discover whether one distribution is relatively more variable than another, it follows that it is necessary to find some method to eliminate the basic units. This is achieved by using the CV. Moore (1958) also showed that the CV does not depend on the units of measurement since both the mean and standard deviation are linear functions of the units involved.

Ostle (1954) found that the CV is an ideal device for comparing the variation in two series of data which are measured in two different units (e.g., a comparison of variation in height with variation in weight). Lewis (1963) noted that the CV may be used to compare the dispersion of series measured in different units and that of series with the same units but running at different levels of magnitude. Similarly, CVs have been used to evaluate results from different experiments involving the same units of measure, possibly conducted by different persons (Steel et al., 1997).

Little and Hills (1978, p.18), stated that the variability among experimental units of experiments involving different units of measurements and/or plot sizes can be compared by CVs. Their extrapolation suggested that a lima bean experiment (s = 5.8 seedlings/plot, yield mean of 82.7 seedlings/plot, CV = 7.0%) had 1.8 times more variability among the plots within a treatment than a sugar beet root yield experiment (s = 1.18 t/ac, yield mean of 30.5 t/ac, CV = 3.9%). Snedecor and Cochran (1980, p.37) indicated that the CV is often used to describe the amount of variation in a population.

Gomez and Gomez (1976) stated that the CV is an indication of the degree of precision to which the treatments are compared and is a good index of the reliability of the experiment. Gomez and Gomez (1976, p. 17) further indicated that the higher the CV value, the lower is the reliability of the experiment.

Work by McClave and Benson (1988) indicated that it is common for the standard deviation of a random variable to increase proportionally as the mean increases. Snedecor and Cochran (1980, p. 37) indicated that the CV is often used to describe the amount of variation in a population. For data from different populations or sources, the mean and standard deviation often tend to change together so that the CV is relatively stable or constant (Snedecor and Cochran, 1980, p. 37). Steel et al. (1997) stated that the CV is a relative measure of variation, in contrast to the standard deviation, which is in the same units as the observation.

Ostle (1954) indicated that experimental error essentially reflects in each particular instance all the extraneous sources of variation which, by their occurrence, help to disguise the true effect of the "treatments" under examination.

The objective of this study was to examine the relationships between mean square errors, yield means, coefficients of variation and plot size using statistical information compiled from past wheat field research projects.

Data from 362 wheat field experiments were targeted for additional statistical analysis. From this population of experiments, 220 were fertilizer, weed management and tillage trials and 142 were variety trials. All experiments were conducted by field researchers, included more than two replications from past M.S. and Ph.D. thesis and published wheat field research projects (Agronomy Journal, Crop Science, and Soil Science Society of America Journal). From each experiment the following information was obtained: number of replications, number of treatments, plot size, CV, degrees of freedom in the error term, mean square error (variance), mean yield, and the standard error of the difference between two treatment means. If all of the above information was not reported, back calculation of the missing term was accomplished when possible (e.g., yield mean determined from the reported CV and MSE). Data for the variables mentioned was only collected for wheat grain yield. The type of experiment was recorded into four separate groups: soil fertility, weed management, tillage and variety trials. From these groups, soil fertility, weed management and tillage trials were combined into a separate group apart from the variety trials due to distinct differences in plot size. Average plot sizes for the fertility/weed/tillage and variety trials were 37.2±24.3 and 3.59±3.13 m2, respectively.

Where necessary, all experimental results were converted into metric units. Correlation matrices were established between all variables collected and simple linear regression equations were determined for specific relationships.

This work assumes that residual mean square error (MSE) from analysis of variance is the best estimate of experimental error or the variability present in a given field experiment. Since all of these data are from similar experiments, MSEs can be compared in order to ascertain the relative variability from experiment to experiment.

In general, when the sums of squares for all independent effects included in an experiment are accounted for in the model, residual error and experimental error are considered to be synonymous. Very few of the experiments reported CVs that exceeded 30%; therefore, grouping experiments with CVs less than 30% was not attempted.

Linear Relationships

No distinct relationship was found between MSE and plot size for either group (Figures 1 and 2). However, there was a tendency for MSE to decrease when plot sizes were between 30 and 100 m2 and 6 and 20m2 for the fertility/weed/tillage and variety data, respectively. Previous work by Barreto and Raun, (1990), which evaluated corn field experiments conducted in Mexico, demonstrated that increasing plot size decreased mean square errors.

Mean yield and CV were negatively correlated for both groups (Figures 1 and 2). Because site mean yields are used as the divisor in calculating CVs, increasing mean yields were expected to produce smaller coefficients of variation.

No highly significant linear relationship could be established between MSE and CV for the fertilizer/weed/tillage trials (Figure 1). Alternatively, MSE and CV were positively correlated for the variety trials. Assuming that the mean square error from analysis of variance is the best measure of variability for field experimentation, and because CVs are considered to be a relative measure of variation (Steel et al., 1997), MSE and CV were expected to be highly correlated. Because this was not the case for the fertilizer/weed/tillage trials, this work demonstrates that CVs are not measuring what some researchers are expecting in field trials. However, there was one critical difference between the fertilizer/weed/tillage trials and the variety trials, and that was plot size which averaged 37.2 and 3.59 m2, respectively.

How could plot size affect the relationship between MSE and CV? Work by Solie et al. (1996) and Raun et al. (1998) attempted to establish the fundamental field element size (area to which an independent rate of a nutrient should be applied). The fundamental field element size is essentially the resolution or scale where detectable differences in soil test parameters exist and that should ultimately be treated differently. Solie et al. (1996) reported that in order to optimize nutrient inputs, areas of 1.96m2 should be treated independently, largely because of significant microvariability in soil test parameters found in soils (Raun et al., 1998). CVs and MSEs were positively correlated in variety trials because the plot size was smaller than those in the fertilizer/weed/tillage trials and nearer the size recommended by Solie et al. (1996). We believe this positive relationship occurs for two reasons. First, the small plot size allows for a better estimate of MSE and minimizes the intra-plot variability. Secondly, smaller plot sizes will reduce the variability encountered in the estimation of the mean, thus reducing the problems experienced by changes in the mean affecting the CV. Alternatively, the fertilizer/weed/tillage trials had average plot sizes 10 times greater than the variety trials, which may have led to the apparent independence of MSE and CV.

Although MSE and CV were positively correlated in the variety trials, the presence of an equally significant negative correlation between CV and mean yield (for both groups, Figures 1 and 2) suggests that CVs were influenced by the environment (mean yield being an indicator of the environment or environment mean). This trait (increasing mean yield and decreasing CV), is not desirable when using the CV as a measure of variability. It is important to remember that the CV is a measure of relative variability. Even though an increase in mean yield will usually result in a corresponding increase in MSE, no linear relationship was found between mean yield and MSE for either of the groups evaluated (Figures 1 and 2). The lack of a significant linear relationship between mean yield and MSE clearly shows why weak relationships between CV and MSE were found since the mean yield entered into the calculation of CV. These results would incorrectly suggest that experimental variability could be reduced simply by increasing the mean yield. For similar types of trials, comparing MSE's (residual error or variance) would be more appropriate in terms of assessing experimental variability since CVs were greatly influenced by the value of the mean yield. The CV would be an appropriate measure for comparing the variation differences in experiments that have variables measured in different units.

The CV is useful when comparing the experimental variation differences in experiments that have variables measured in different units. A researcher must remember that the CV is measuring relative variability and that it has an inverse relationship with the sample mean. If one wishes to compare the experimental variation of trials containing variables with common units, the MSE would be the appropriate measure to use. The lack of a strong relationship between MSE and CV should cause concern for researchers using the CV as a measure of the 'reliability of the experiment' or to compare results from different experiments involving the same units of measure. The smaller plot size employed in plant breeding variety trials (average of 3.59m2) when compared to the fertilizer/weed/tillage trials (average of 37.2m2) reduced the variability encountered in the estimation of the mean. The smaller plot size employed in the variety trials is considered to be advantageous in field plot work since it is consistent with the resolution where detectable differences in soil test parameters exist and that should be treated independently.

Barreto, H.J., and W.R. Raun. 1990. La precision experimental de los ensayos regionales con maiz (Zea mays L.) a traves de centroamerica. In Programa regional de maiz para Centro America, Panama y El Caribe. CIMMYT, Mexico D.F., 06600.

Chaddock, R.E. 1925. Principles and methods of statistics. 1st ed. Houghton Mifflin Co., Cambridge MA.

Gomez K.A., and A.A. Gomez. 1984. Statistical procedures for agricultural research. 2nd ed. John Wiley and Sons, New York, NY.

Lewis E.E. 1963. Methods of statistical analysis in economics and business. 2nd ed. Houghton Mifflin Co., Boston, MA.

Little, Thomas M., and F. Jackson Hills. 1978. Agricultural experimentation. John Wiley and Sons, New York, NY.

McClave, James T., and P. George Benson. 1988. Statistics for business and economics. Dellen Publishing Co., San Francisco, CA.

Mills, F.C. 1924. Statistical methods. 3rd ed. Henry Holt and Co., New York, NY.

Moore, P.G. 1958. Principles of statistical techniques. 1st ed. Cambridge at the Univ. Press, New York, NY.

Ostle, B. 1954. Statistics in research basic concepts and techniques for research workers. 1st ed. Iowa State College Press, Ames, IA.

Raun, W.R., J.B. Solie, G.V. Johnson, M.L. Stone, R.W. Whitney, H.L. Lees, H. Sembiring, and S.B. Phillips. 1998. Microvariability in soil test, plant nutrient, and yield parameters in bermudagrass. Soil Sci. Soc. Am. J. 62:683-690.

Senders, V.L. 1958. Measurement and statistics. 1st ed. Oxford University Press, New York, NY.

Snedecor, George W., and William G. Cochran. 1980. Statistical methods. 7th ed. The Iowa State Univ. Press, Ames, IA.

Solie, J.B., W.R. Raun, R.W. Whitney, M.L. Stone and J.D. Ringer. 1996. Optical sensor based field element size and sensing strategy for nitrogen application. Trans. ASAE 39(6):1983-1992.

Steel, Robert G.D., James H. Torrie, and David A. Dickey. 1997. Principles and procedures of statistics, a biometrical approach. 3rd ed. McGrawHill Book Co., New York, NY.

Tippett, L.H. 1952. The methods of statistics. 4th ed. John Wiley & Sons, Inc., New York, NY.

Zar, J.H. (1984) Biostatistical Analysis. 2nd ed. PrenticeHall, Inc., Englewood Cliffs, N.J.

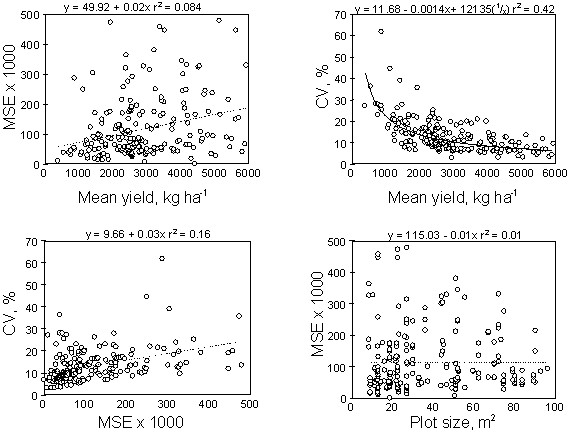
FIGURE 1. Relationship between mean yield, mean square error (MSE), coefficient of variation (CV) and plot size from 220 fertilizer, weed management and tillage trials.

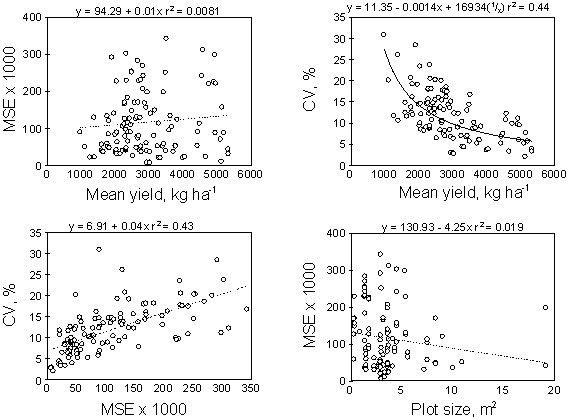
FIGURE 2. Relationship between mean yield, mean square error (MSE), coefficient of variation (CV) and plot size from 142 variety trials.