W.R. Raun, J.B. Solie, G.V. Johnson, M.L. Stone, E.V. Lukina, W.E. Thomason and J.S. Schepers
Dep. of Plant and Soil Sciences, and Dep. of Biosystems and Agricultural Engineering, Oklahoma State University, Stillwater, OK 74078; USDA-ARS, Lincoln, NE. Contribution from the Okla. Agric. Exp. Stn.
Abstract
Nitrogen fertilization rates in cereal production systems are
generally determined by subtracting soil test N from a specified grain yield
goal-based N requirement, where yield goal represents the best achievable grain
yield in the last four to five years. If grain yield could be predicted
in-season, topdress N rates could be adjusted based on projected N removal. Our
study was conducted to determine if winter wheat (Triticum aestivum L.)
potential grain yield could be predicted using in-season spectral measurements
collected between January and March. The normalized difference vegetation index
(NDVI) was determined from reflectance measurements under daytime lighting in
the red and near infrared regions of the spectra. In-season estimated yield (EY)
was computed using the sum of two post-dormancy NDVI measurements (January and
March), divided by the cumulative growing degree days from the first to second
reading. A significant relationship between grain yield and EY was observed
(R2 = 0.50, PR>F 0.0001) when combining all nine locations across a two-year
period. Our estimates of potential grain yield (made in early March) differed
from measured grain yield (mid July) at three sites where yield-altering factors
(e.g., late summer rains delayed harvest and increased grain yield loss due to
lodging and shattering) were encountered after the final sensing. Evaluating
data from six of the nine locations across a two-year period, EY values
explained 83 % of the variability in measured grain yield. Use of EY may
assist in refining in-season application of fertilizer N based on predicted
potential grain yield.
Introduction
Historically, grain yield goals have been the most reliable method available for estimating pre-plant fertilizer N rates. Recent advancements in weather forecasting and crop modeling have enabled the development of technologies for predicting potential grain yields thus allowing for in-season nutrient adjustment to reflect early crop development and growing conditions.
Yield Goals
Crop grain yield may be expressed simply as a function of all conditions of the
growing environment, or growth factors, and any preconceived yield goal or limit
set by management. In dryland agriculture, it is usually advantageous to set the
grain yield goal above that of average yields in order to fully take advantage
of above-average growing conditions (Johnson, 1991). Yield goal was defined by
Dahnke et al. (1988) as the 'yield per acre you hope to grow.' They further
noted that what you hope to grow and what you end up with are two different
things. Yield goals can vary all the way from past average yield to potential
yield (Dahnke et al., 1988). They defined potential grain yield as the highest
possible yield obtainable with ideal management, soil, and weather. In our work,
what they define as potential grain yield would be maximum grain yield, since
'potential' yield is associated with specific soil and weather conditions that
can change annually. For most farmers, North Dakota State University recommends
that the grain yield goal is the highest yield attained in the last four to five
years and that it is usually 30 to 33% higher than the average yield (personal
communication, R. J. Goos, 1998).
Rehm and Schmitt (1989) noted that with favorable soil
moisture at planting it would be smart to aim for a 10 to 20% increase over the
recent average when selecting a grain yield goal. They also indicated that if
soil moisture is limiting, use of history and past maximums (used to generate
averages) may not be the best method for setting a grain yield goal for the
upcoming crop. Use of farm and/or county averages was not suggested for
progressive farmers concerned with high farm profitability (Rehm and Schmitt,
1989).
Black and Bauer (1988) reported that the grain yield goal
should be based on how much water is available to the winter wheat crop from
stored soil water to a depth of 1.5 m in the spring plus the anticipated amount
of growing season precipitation. Combining grain yield goal, soil test NO3-N and
a simple estimate of nitrogen use efficiency can be used to estimate N
fertilization requirements. Several states recommend that farmers apply 33 kg N
ha-1 for every 1 Mg of wheat (2 lb N ac-1 for every bushel of wheat) they hope
to produce, minus the amount of NO3-N in the surface (0-15 cm) soil profile
(Johnson et al., 1997). Therefore, when grain yield goals are applied, it
explicitly places the risk of predicting the environment (good or bad year) on
the producer. University extension (e.g., soil testing), fertilizer dealers and
private consulting organizations have historically used grain yield goals, due
to the lack of a better alternative.
In-Season Soil Testing
Initial work by Magdoff et al. (1984) evaluated the use of an
in-season NO3-N soil test for corn by sampling soils to 30 cm when plants are
15-30 cm tall. This test, which was later referred to as the pre-sidedress
nitrate test (PSNT), was useful for predicting N needs in the Northeastern
portions of the USA. The benefits of PSNT over yield goals to recommend N for
corn (Zea mays L.) was shown by Durieux et al. (1995), where less N was applied
with no reduction in grain yield. Sims et al. (1995) indicated that the leaf
chlorophyll meter could be an alternative to the PSNT for refining in-season
fertilizer N requirements in maize. Spellman et al. (1996) showed that the
critical PSNT ranged between 13 and 15 mg N kg-1 for the 0-30 cm soil sampling
depth, for irrigated corn grown in a semi-arid environment in Colorado, well
below the 21 mg N kg-1 suggested for humid regions of the USA. Bundy and
Andraski (1995) indicated that separating nitrate test data according to the
potential yield of soils (medium and high based on depth of root zone, water
holding capacity and length of growing season) may improve the utility of the
preplant nitrate test (PPNT) and PSNT for making N recommendations for corn when
soil test values are in the N responsive region.
Fox et al. (1993) evaluated PSNT, near-infrared
spectrophotometer reflectance from soil samples taken at planting, and an
at-planting soil nitrate test for use in predicting grain yield and soil
N-supplying capability. These methods did not predict relative grain yield or
the potential to supply N. However, they noted that near-infrared preplant soil
testing did predict whether or not humid-region corn fields would respond to N
fertilizer.
Use of Indirect Measures for Grain Yield
Prediction
Estimating crop yields is an important application of remote
sensing (Lillesand and Kiefer, 1994; Moran et al., 1997). The normalized
difference vegetation index (NDVI), calculated with measurements of reflected
light from the red and near-infrared bands, has long been used as an indirect
measure of crop yield, including that of wheat (Colwell et al., 1977; Tucker et
al., 1980; Pinter et al., 1981). Aase and Siddoway (1981) confirmed the
relationship of NDVI to wheat grain yield but noted that the relationship
deteriorated rapidly as wheat ripened. Soil background, view and solar angles,
atmospheric conditions, and crop canopy architecture are also important factors
affecting NDVI (Huete, 1987; Jackson and Huete, 1991). Pinter et al. (1981)
reported that summing NDVI values from late-season (Feekes 10.5, flowering to
grain fill) spectral measurements was useful in predicting wheat grain yield.
Bartholome (1988) reported that accumulated NDVI was a more stable predictor of
millet and sorghum grain yields than a single spectral measurement. Rasmussen
(1992) calculated a sampling-interval weighted average NDVI by integrating
multi-temporal spectral measurements with time, which improved millet grain
yield estimates from a single spectral measurement. Smith et al. (1995) reported
that sensing twice and combining NDVI using a linear model improved correlation
with wheat grain yield compared to sensing once. Rasmussen (1998) failed to
improve the correlation of NDVI to grain yield by integrating the product of
multi-temporal NDVI measurements and photosynthetically active radiation (PAR).
Definitions of Measured Grain Yield,
Potential, and Maximum Grain Yields
Measured grain yield is that actually harvested in a given
year at a given site (independent of scale). Potential grain yield is that
predicted for a given year and site, based on the assumption that the level of
growth factors responsible for early development of the crop will be maintained
(limitations that existed at early stages of growth will continue to similarly
influence development to maturity, e.g., N deficiency). Maximum grain yield is
that achievable when all manageable growth factors (nutrients, insects, disease,
weeds, etc) are non-limiting and the environment is ideal. Depending on the
environment, potential grain yield would always be maximum grain yield.
Prediction of Biomass and Percent Coverage
Recent work has shown that NDVI measurements in winter
wheat between Feekes physiological growth stages 4 and 5 can provide reliable
prediction of both N uptake and biomass (Stone et al., 1996; Solie et al.,
1996). The percentage of soil covered by wheat was highly correlated with NDVI
at Feekes physiological growth stages 4 and 5, and both NDVI and coverage were
correlated with vegetative biomass (Lukina et al., 1999). In these trials, plant
coverage was generally > 50% at Feekes 4 and 60% at Feekes 5. Similar work by
Reeves et al. (1993) used direct in-season measurements of total N uptake in
winter wheat at Feekes growth stage 5 to predict grain yield.
Much of the work associated with making fertilizer recommendations has not
considered the potential for using in-season prediction of potential grain
yield. Therefore, the objective of this work evaluated the use of early-season
red and near infrared spectral reflectance field measurements of wheat tissue
combined with growing degree days to predict potential grain yield.
Materials and Methods
During the winter months of 1998 and 1999, spectral
reflectance readings were taken from nine winter wheat experiments. Each
experiment was either an on-going long-term experiment (numbers assigned in the
1960's and 1970's as 222, 301, 502 and 801), or a short-term (1-3 years) field
experiment that included the evaluation of preplant N rates. Each of these
locations, is further defined in Table 1. The soils at each of these locations
follow; Perkins, Teller sandy loam (fine-loamy, mixed, thermic Udic Argiustolls);
Tipton, Tipton silt loam (fine-loamy, mixed, thermic Pachic Argiustolls);
Stillwater, Kirkland silt loam (fine, mixed, thermic Udertic Paleustolls);
Stillwater-Efaw, Norge silt loam (fine-silty, mixed, thermic Udic Paleustolls);
Lahoma, Grant silt loam (fine-silty, mixed, thermic Udic Argiustolls); and
Haskell, Taloka silt loam (fine, mixed, thermic Mollic Albaqualfs). The row
spacing by N rate (S*N) and Efaw anhydrous ammonia (AA) experiments were each
one-year trials. The N rate by P rate (N*P) experiment at Perkins was initiated
in 1996. Experiments 222, 301 and 502 were initiated in 1969, 1993 and 1971,
respectively, and all three evaluated annual rates of applied N at constant
levels of P and K (Table 1). Winter wheat was planted at a 78 kg ha-1 seeding
rate using a 0.19 m row spacing, excluding the S*N experiment at Perkins
(spacing ranged from 0.15 to 0.30 m).
Spectral reflectance was measured using an instrument that
included two upward directed photodiode sensors that received light through
cosine corrected Teflon windows fitted with red (671+/-6nm) and near-infrared (NIR)(780+/-6nm)
interference filters. The instrument also included two down-looking photodiode
sensors that received light through collination and interference filters
identical to the up-looking sensors. The instrument used a built in 16 bit A/D
converter that converted the signals from all four photodiode sensors
simultaneously. The collination was configured to constrain the view of the
down-looking sensors to a 0.84 m2 oblong area at the plant surface. Stability of
the sensor was maintained across time through calibration using a barium sulfate
coated aluminum plate. The reflectance of the barium sulfate coated plate was
assumed to be 1.0 for both spectral bands investigated.
All experiments included in this study are described in Table
1. Varietal differences were not targeted in this work because the findings of
Sembiring et al. (2000) showed limited differences in post-dormancy NDVI
readings for common wheat varieties grown in this region. Reflectance readings
from all experiments were collected at two post-dormancy dates. The two dates
(Time-1 and Time-2, respectively) where readings were collected generally
corresponded to Feekes growth stage 4 (leaf sheaths beginning to lengthen) and 5
(pseudo-stem, formed by sheaths of leaves strongly erect) (Large, 1954). Due to
differences in planting times and growing conditions, spectral reflectance
readings were collected between January and March (Table 1). All reflectance
readings from wheat were taken from a 4.0 m2 area between 10 a.m. and 4 p.m
under natural lighting.
Reflectance values (the ratio of incident and reflected
values) were used in the NDVI calculation to minimize the error associated with
cloud cover, shadows and sun angle. The modified equation used was; NDVI = [(NIRref/NIRinc)-(Redref/Redinc)]
/ [(NIRref/NIRinc)+(Redref/Redinc)], where NIRref and Redref = magnitude of
reflected light, and NIRinc and Redinc = magnitude of the incident light.
In both years, grain yield was determined using a self
propelled combine from the same 4.0 m2 area where spectral reflectance data were
collected. We assumed that growth from planting in October to the mid winter
months of January and February would provide an excellent indicator of wheat
health in each 4.0 m2 area and thus the early-season growth-limiting conditions
for small areas. The sum of NDVI at Time-1 and NDVI at Time-2, divided by
growing degree days between the two dates (GDD = [(Tmin + Tmax)/2 - 4.4C] (Tmin
and Tmax recorded from daily data) was computed and evaluated as an index for
in-season prediction of potential grain yield (in-season estimated yield, or EY). Minimum and maximum air temperatures, and rainfall data were collected
within 1.7 km of the actual experiment at all locations.
The EY index was one of many indices evaluated that included mathematical
combinations of the following; NDVI at Time-1 and Time-2, GDD and total days
from Time-1 to Time-2, GDD and total days from planting to Time-1, and GDD and
total days from planting to Time-2. The EY value was expected to reflect a
point on the potential growth curve for that season, thus providing an estimate
of potential grain yield based on local growing conditions between planting and
the dates of sensing. This index was found to include all sites, and had a high
combined r2 when compared to the many other indices tested.
Measured grain yield was considered to be the best available
measure of potential grain yield, especially where limited stress occurred after
sensor readings in late February and early March. The use of GDD in the
computation of EY allowed us to integrate early season growing conditions and
growth rate. This approach is consistent with work by Rickman et al. (1996)
showing the relationship between above ground dry mass and cumulative growing
degree days (Fig. 1). Dividing the sum of NDVI at Time-1 and Time-2 by GDD
results in a unit of predicted biomass (using NDVI) per growing degree day.
Linear, quadratic, logarithmic and exponential models were
evaluated that included all locations and data subsets using various indices to
predict measured grain yield. In addition, confidence limits were established
for point estimates about regression lines for those models that best fit the
data.
Results
It is important to note that grain yield-limiting factors
associated with post Feekes 5 environments can cause measured grain yields to
differ from predicted potential grain yields. Therefore, it was critical to
identify those sites where obvious yield-limiting or yield-enhancing factors
were present following the final sensor measurement. In this regard, we
recognized that it would be extremely difficult to identify an index that would
reliably predict measured grain yield across nine locations where planting date,
harvest date, sensor dates, rain, and growing degree days differed.
Although many indices were evaluated that included NDVI at Times 1 and 2 (e.g.,
GDD from planting to Time 1 and 2, d from Time 1 and Time 2 and days from
planting), the EY index proved to account for more of the variability in
measured grain yield, especially when sites where post-sensing grain yield
limiting factors were considered. It was not until GDD was used as a divisor
(combined with mid-winter sensor data) that we found models that included the
majority of the nine sites studied. Therefore, regression analysis reported in
this paper focuses on results from EY that included GDD in its calculation.
EY versus Grain Yield (all nine locations)
The relationship between measured grain yield and EY for
all nine locations is illustrated in Fig. 2. Although definite differences were
noted between the nine experiments included in this work, quadratic and
exponential models for the entire data set resulted in coefficients of
determination (r2) > 0.50 and were highly significant (PR>F 0.0001).
Three sites exhibited responses that were markedly different from the rest of
the experiments: Experiment 502 in 1999; N*P Perkins in 1999; and Efaw AA in
1999. When compared to the remaining six locations, Experiment 502 in 1999 and
N*P Perkins in 1999 had lower than expected grain yields and high EY values
(Fig. 2). Combined, data for these two sites alone still showed a good
relationship between EY and grain yield (r2 = 0.78). Plant stands were
excellent following planting at all sites, a result of timely but not excessive
rain, and growing conditions were near ideal prior to sensing. However, at
Experiment 502, 1999, excessive rain delayed grain harvest to 30 June, 1999 (3
to 4 weeks later than normal), and, consequently reduced grain yields because of
lodging and shattering. Had grain harvest taken place on time, we believe that
grain yields would have been much higher and likely to have been similar to the
S*N Tipton data in 1998 (Fig. 2).
Grain yields were much lower than predicted by EY for the
N*P Perkins, 1999 experiment. Although EY values reflected a much higher
potential grain yield, yields were characteristically lower at this site. Forage
growth was excellent early in the season as was plant development up to
flowering. However, without timely rain, the sandy loam soil at this site dries
out quickly and the lower moisture storage becomes more yield-limiting than the
silt loam and clay loam soils at other sites. As a result, measured grain yields
were lower than what would have been predicted using EY, even though plant
stands and growth up to late February were indicative of a higher yielding crop.
Measured grain yields at the Efaw AA, 1999 experiment were higher than what
would have been expected using EY. This experiment was located on an alluvial
portion of the landscape and received added moisture via runoff from adjoining
slopes. Forage growth was abnormally low at this site due to the late (9
November) planting date (Table 1). As a result, potential grain yields estimated
using EY were low, since wheat plants were small when sensed in February and
March. However, forage growth improved significantly later in the season. Late
season wheat growth benefited from the added moisture received via runoff, and a
soil profile that provided ample water during grain fill. We believe these
factors caused potential grain yields to be underestimated using EY.
EY versus Grain Yield (six locations)
When data for the three sites where grain yield was strongly
influenced by abnormal post-sensing conditions (N*P Perkins, 1999; Efaw AA,
1999; and Experiment 502, 1999) were removed, the relationship between measured
grain yield and EY improved (Fig. 3). Including data obtained from these six
locations across a two year period, EY values explained 83 % of the
variability in grain yield (PR>F 0.0001). Two of the six experiments included
in this data set were 450 km apart, and rain from planting to harvest ranged
from 645 mm (S*N Tipton, 1998) to 1016 mm (Experiment 801, 1999). Considering
the range of factors that affect final grain yield, and the influence of
environment from Time-2 to maturity, we considered it important to find an index
that closely predicted potential grain yield.
In our work, all data were combined in an attempt to derive a
single standard curve to predict potential grain yield for the purpose of
variably applying nitrogen fertilizer. This is noteworthy considering the wide
range in NDVI values found at all locations at Feekes growth stages 4 and 5
(Table 2). The only adjustment to the sum of NDVI values from Feekes growth
stage 4 to 5 was the division of this sum by GDD between the two measurements.
This divisor was expected to partially account for growing conditions when
combining sites and years. Considering the many non-controllable environmental
factors that can influence final grain yield (after spectral data was acquired),
we were willing to tolerate some error if it would enable using a single curve
to estimate potential grain yield across a range of conditions. This is
important if algorithms are to be developed that minimize the need to
recalibrate the sensor/fertilizer controller for changing conditions within a
field or between fields. Predicted mean grain yield of the six experiments used
to develop the standard curve in Fig. 3 fell within ±14% of the average
measured grain yields (Table 3). Linear regression of predicted mean grain yield
on measured mean grain yield for the subset of 6 locations discussed previously,
and all 9 locations had r2 of 0.98 (PR>F, 0.01) and 0.33 (PR>F, 0.10),
respectively. For these same models, slopes were not significantly different
from 1, and intercepts were not different from 0. We believe these errors are
tolerable in estimating potential grain yield if the benefits of variable
applying topdress N fertilizer can still be obtained. Experience may identify
sites where the sensor consistently over or underestimates potential grain
yield, and the calibration can be reliably adjusted.
Discussion
It is important to note that the sum and not the difference
in NDVI from Time-1 to Time-2 was used since the sum would reflect the average,
while the difference (NDVI at Time-2 minus NDVI at Time-1) would theoretically
take into account growth rate. Although we were interested in growth from Time-1
to Time-2, the difference in NDVI from Time-1 to Time-2 was inconsistent since
some measurements resulted in negative values. This was a biological possibility
in winter wheat; especially considering what can happen in terms of weather from
January to February and its effect on wheat foliage. This is in addition to
other factors affecting optical measurements enumerated by Huete (1987) and
Jackson and Huete (1991). The sum of NDVI at Time-1 and Time-2 was used because
the initial prediction of biomass (Time-1) integrated growing conditions and
plant health (stand density, vigor and N uptake) from planting until the first
winter spectral reading. Also, adding the two NDVI readings (estimates of
biomass) assisted in removing some of the variability in radiometric data
collected from the same 1 m2 area at different times, and that would be
influenced by changing soil moisture (reduced NIR and increased red
reflectance). Pinter et al. (1981) reported that summing NDVI values assisted in
predicting grain yield, however, their work employed spectral readings that were
first collected at flowering (Feekes 10.5) and proceeded to senescence. Our
approach was to collect sufficient information prior to Feekes 5 (60-90 days
before flowering) that could be used to predict potential grain yields, and in
time to apply fertilizer N without damaging the crop.
Data collected in the 1998 and 1999 growing seasons were unique since adequate
moisture was present at planting, and continued throughout each growing season.
Only limited moisture stress was present, and all sites received timely rain
near flowering. For this reason, measured grain yield and potential grain yield
were expected to be similar for 1998 and 1999, and this we believe contributed
strongly to our finding a high correlation of EY with measured grain yield at
six locations. We would not expect EY to be highly correlated with measured
grain yield in all growing seasons, since so many things can happen to the wheat
crop from post-dormancy to maturity (frost, disease, drought, etc.). However,
our interest was in developing a yield parameter that was seasonal-sensitive,
intrinsic, and that would reflect the potential grain yield likely to be
realized in that season than traditional yield goal estimates. If growth was
poor from planting to Time-2, it is unlikely that a high potential grain yield
would be realized. Similarly, if growth was excellent from planting to
post-dormancy, but declined from the first to second reading (Time-1 to Time-2,
drought, frost damage, etc.), potential grain yield would be expected to be
lower.
The 10 to 40 d period immediately following dormancy is
critical in terms of the resulting grain yield. Obtaining two sensor readings
during this period provides a measure of crop development and growing
conditions. Unlike growth models that rely on various inputs to predict plant
growth, optical sensing uses the plant as the indicator. The first reading
establishes a base measurement of crop condition and the second reading assesses
post dormancy change across a short, measured time period. Combined, these two
readings and the adjustment for GDD should provide a reasonable indication of
potential grain yield. Typically, early-season growing condition information is
accessed by the first reading in late February. The period from planting (mid
October) to the end of dormancy (late February) represents more than half the
growing season and provides potential grain yield information. Once potential
yield is determined, topdress N rates could be adjusted based on projected grain
N removal. Sensing beyond Feekes physiological stage 5 (Time-2) is not practical
for winter wheat grown in the United States since significant stand damage is
encountered when topdress equipment is used for N applications following this
time.
When spatially precise estimates of potential grain yield are
made, these estimates will be determined at the finest resolutions (1 m2) where
differences in soil test parameters are found (Solie et al., 1996; Solie et al.,
1999). At coarser resolutions (>30 m), the variation in potential grain yield
will be masked by averaging and benefits that may have been realized in treating
the variability can be lost. Thus, one of the reasons why we found such good
correlation between EY and measured grain yield (or potential grain yield)
was because we were operating at a resolution of 4 m2. In this regard, topdress
N rates based on in-season prediction of potential grain yield must take place
at the same resolution where spatial variability is encountered.
Conclusions
We propose the use of two post dormancy spectral reflectance
readings (NDVI collected at or near Feekes growth stage 4 and again at Feekes
growth stage 5) to assess the initial status of plant growth from planting to
the end of dormancy, and post dormancy growth across a short time period
(January to March). Adding these two NDVI readings, and dividing by the growing
degree days between readings provides an indication of what potential grain
yield should be for a wide range of growing conditions, planting times and
sensing dates. For the two years evaluated, measured grain yield and estimated
potential grain yield or EY were expected to be similar, since the dryland
growing conditions were near-ideal throughout the season. Including data
obtained from six locations for a two-year period, EY values explained 83 %
of the variability in grain yield and thus an early-season indication of
potential grain yield (measured grain yield used as the indicator variable)
across a range of growing environments.
Acknowledgements
The authors wish to thank J.M. LaRuffa, S.B. Phillips, J.L. Dennis, D.A. Cossey,
M.J. DeLeon, C.W. Woolfolk, R.W. Mullen, B.M. Howell, and Jing Wang for their
assistance with field and lab work.
References
Aase, J.K., and F.H. Siddoway. 1981. Assessing winter wheat dry matter
production via spectral reflectance measurements useful in providing an estimate
of residue production for erosion control and as a potential source for feed and
energy. Remote Sensing of Environ. 11:267-277.
Bartholome, E. 1988. Radiometric measurements and crop yield forecasting: some observations over millet and sorghum experimental plots in Mali. Int. J. Remote Sensing. 9:1539-1552.
Black, A.L., and A. Bauer. 1988. Setting winter wheat yield goals. In J.L. Havlin (ed.) Central Great Plains Profitable Wheat Management Workshop Proc. Wichita, KS. Aug. 17-20, 1988. Potash & Phosphate Institute, Atlanta, GA.
Bundy, L.G., and T.W. Andraski. 1995. Soil potential yield effects on performance of soil nitrate tests. J. Prod. Agric. 8:561-568.
Colwell, J.E., D.P. Rice, and R.F. Nalepka. 1977. Wheat yield forecasts using Landsat data. Proc. 11th International Symposium on Remote Sensing of Environment. Ann Arbor MI p. 1245-1254.
Dahnke, W.C., L.J. Swenson, R.J. Goos, and A.G. Leholm. 1988. Choosing a crop yield goal. North Dakota State Ext. Serv. SF-822. Fargo, North Dakota.
Durieux, R.P., H.J. Brown, E.J. Stewart, J.Q. Zhao, W.E. Jokela and F.R. Magdoff. 1995. Implications of nitrogen management strategies for nitrate leaching potential: roles of nitrogen source and fertilizer recommendation system. Agron. J. 87:884-887.
Fox, R.H., J.S. Shenk, W.P. Piekielek, M.O. Westerhaus, J.D. Toth, and K.E. Macneal. 1993. Comparison of near-infrared spectroscopy and other soil nitrogen availability quick tests for corn. Agron. J. 85:1049-1053.
Huete, A.R. 1987. Soil-dependent spectral response in a developing plant canopy. Agron. J. 79:61-68.
Jackson, R.D., and A.R. Huete. 1991. Interpreting vegetation indices. Prev. Vet. Med. 11:185-200.
Johnson, G.V. 1991. General model for predicting crop response to fertilizer. Agron. J. 83:367-373.
Johnson, G.V., W.R. Raun, H. Zhang, and J.A. Hattey. 1997. Soil fertility handbook. Okla. Agric. Exp. Sta. Stillwater, OK.
Large, E.C. 1954. Growth stages in cereals. Illustration of the Feekes Scale. Plant Pathol. 3:128-129.
Lillesand, T. M., and R. W. Kiefer. 1994. Remote Sensing and Image Interpretation, 3rd Ed. New York: John Wiley & Sons, Inc.
Lukina, E.V., M.L. Stone, and W.R. Raun. 1999. Estimating vegetation coverage in wheat using digital images. J. Plant Nutr. 22:341-350.
Magdoff, F.R., D. Ross, and J. Amadon. 1984. A soil test for nitrogen availability to corn. Soil Sci. Soc. Am. J. 48:1301-1304.
Moran, M.S., Y. Inoue, and E.M. Barnes. 1997. Opportunities and limitations for image-based remote sensing in precision crop management. Remote Sens. Environ. 61:319-346.
Pinter, P.J., Jr., R.D., R.D. Jackson, S.B. Idso, and R.J. Reginato. 1981. Multidate spectral reflectance as predictors of yield in water stressed wheat and barley. Int. J. Remote Sensing. 2(1):43-48.
Rasmussen, M.S. 1992. Assessment of millet yields and production in northern Burkina Faso using integrated NDVI from AVHRR. Int. J. Remote Sensing. 13(18):3431-3442.
Rasmussen, M.S. 1998. Developing simple operational consistent NDVI-vegetation models by applying environmental and climatic information. Part II: crop yield assessment. Int. J. Remote Sensing. 19(1):119-139.
Reeves, D.W., P.L. Mask, C.W. Wood, and D.P. Delaney. 1993. Determination of wheat nitrogen status with a hand-held chlorophyll meter: influence of management practices. J. Plant Nutr. 16:781-796.
Rehm, George, and Michael Schmitt. 1989. Setting realistic crop yield goals. Minnesota Ext. Serv. AG-FS-3873, Univ. of Minnesota, 55108.
Rickman, R.W., Sue E. Waldman, and Betty Klepper. 1996. MODWht3: A development-driven wheat growth simulation. Agron J. 88:176-185.
Sembiring, H., H.L. Lees, W.R. Raun, G.V. Johnson, J.B. Solie, M.L. Stone, M.J. DeLeon, E.V. Lukina, D.A. Cossey, J.M. LaRuffa, C.W. Woolfolk, S.B. Phillips, and W.E. Thomason, . 2000. Effect of growth stage and variety on spectral radiance in winter wheat. J. Plant Nutr. 23:141-149.
Sims, J.T., B.L. Vasilas, K.L. Gartley, B. Milliken, and V. Green. 1995. Evaluation of soil and plant nitrogen tests for maize on manured soils of the Atlantic Coastal Plain. Agron. J. 87:213-222.
Smith, R.C.G., J. Adams, D.J. Stephens, and P.T. Hick. 1995. Forecasting wheat yield in mediterranean-type environment from NOAA Satellite. Aust. J. Agric. Res. 46:113-25.
Solie, J.B., W.R. Raun, R.W. Whitney, M.L. Stone and J.D. Ringer. 1996. Optical sensor based field element size and sensing strategy for nitrogen application. Trans. ASAE 39(6):1983-1992.
Solie, J.B., W.R. Raun, and M.L. Stone. 1999. Submeter spatial variability of selected soil and bermudagrass production variables. Soil Sci. Soc. Amer. J. 63:1724-1733.
Spellman, D.E., A. Rongni, D.G. Westfall, R.M. Waskom, and P.N. Soltanpour. 1996. Pre-sidedress nitrate soil testing to mange nitrogen fertility in irrigated corn in a semi-arid environment. Commun. Soil Sci. Plant Anal. 27:561-574.
Stone, M.L., J.B. Solie, W.R. Raun, R.W. Whitney, S.L. Taylor, and J.D. Ringer. 1996. Use of spectral radiance for correcting in-season fertilizer nitrogen deficiencies in winter wheat. Trans. ASAE 39(5):1623-1631.
Tucker, C.J., J.H. Elgin, Jr., J.E. McMurtrey
III. 1980. Realtionship of spectral data to grain yield variation.
Photogrammetric Engineering and Remote Sensing. 46(5):657-666.
Table 1. Experiments where sensor and winter wheat grain yield data were collected, location, number of plots, growth stage, and sampling date. ______________________________________________________________________________________________ Experiment Location Year No. Dates Days GDD‡ Planting Harvest Variety -----------Rainfall--------- of plots Sensed T1 to T1 to date date planting planting T2 sensed (T1 & T2) T2† T2† to to T2 to maturity maturity ------------ mm ----------- S*N§ Perkins, OK 1998 48 24/2/98 42 187 21/10/97 15/6/98 Tonkawa 638 396 242 6/4/98 S*N§ Tipton, OK 1998 48 27/1/98 31 120 7/10/97 3/6/98 Tonkawa 415 277 138 26/2/98 N*P Perkins, OK 1998 36 24/2/98 38 154 21/10/97 15/6/98 Tonkawa 638 396 242 2/4/98 N*P Perkins, OK 1999 12 12/2/99 21 99 12/10/98 9/6/99 Tonkawa 655 244 411 4/3/99 Experiment 222 Stillwater, OK 1999 20 18/1/99 38 153 13/10/98 15/6/99 Tonkawa 759 305 454 24/2/99 Experiment 301 Stillwater, OK 1999 18 19/2/99 34 142 15/10/98 15/6/99 Tonkawa 759 309 450 24/3/99 Efaw AA Stillwater-Efaw, OK 1999 21 19/2/99 34 142 9/11/98 15/6/99 Tonkawa 596 146 450 24/3/99 Experiment 502 Lahoma, OK 1999 28 10/2/99 24 96 9/10/98 30/6/99 Tonkawa 882 337 545 5/3/99 Experiment 801 Haskell, OK 1999 28 16/2/99 36 189 16/10/98 6/7/99 2163 1016 600 416 23/3/99 ____________________________________________________________________________________________________________________ †T1 to T2, (d/m/yr) Time-1 (Feekes growth stage 4) to Time-2 (Feekes growth stage 5) ‡GDD, growing degree days calculated as the daily sum of (Tmin + Tmax)/2 - 4.4°C. §S*N, row spacing by N rate experiment N*P, N rate by P rate experiment
Table 2. Minimum, maximum, and mean values for NDVI collected at Feekes growth stages 4 and 5 and EY, from nine experiments. _______________________________________________________________________________ Exp. Location Year NDVI Feekes 4 NDVI Feekes 5 EY† min max mean min max mean min max mean S*N§ Perkins, OK 1998 0.33 0.64 0.47 0.32 0.76 0.52 0.0035 0.0071 0.0053 S*N§ Tipton, OK 1998 0.50 0.85 0.74 0.60 0.91 0.80 0.0092 0.0146 0.0128 N*P Perkins, OK 1998 0.26 0.76 0.47 0.39 0.86 0.63 0.0047 0.0101 0.0071 N*P Perkins, OK 1999 0.55 0.77 0.66 0.37 0.76 0.56 0.0094 0.0154 0.0123 Exp. 222 Stillwater, OK 1999 0.14 0.60 0.39 0.12 0.74 0.54 0.0041 0.0087 0.0063 Exp. 301 Stillwater, OK 1999 0.31 0.74 0.55 0.23 0.84 0.64 0.0038 0.0110 0.0084 Efaw AA Stillwater-Efaw, OK 1999 0.33 0.62 0.41 0.59 0.80 0.72 0.0068 0.0098 0.0080 Exp. 502 Lahoma, OK 1999 0.40 0.79 0.66 0.41 0.88 0.73 0.0085 0.0174 0.0145 Exp. 801 Haskell, OK 1999 0.42 0.89 0.77 0.35 0.89 0.78 0.0041 0.0093 0.0082 __________________________________________________________________________________ † EY (in-season estimated yield = (NDVI Feekes 4 + NDVI Feekes 5)/growing degree days from Feekes 4 to Feekes 5) Exp-experiment, §S*N, row spacing by N rate experiment N*P, N rate by P rate experiment
Table 3. Predicted, measured and percent of measured mean winter wheat grain yield from nine experiments. _____________________________________________________________________________ Experiment Location Year Measured Predicted Percent mean grain mean grain of measured yield yield† mean grain yield ------- kg ha-1 ------ S*N§ Perkins, OK 1998 1409 1212 86.0 S*N§ Tipton, OK 1998 3999 3911 97.8 N*P Perkins, OK 1998 1752 1654 94.4 N*P Perkins, OK 1999 1932 3622 187.4 Experiment 222 Stillwater, OK 1999 1274 1438 112.8 Experiment 301 Stillwater, OK 1999 1909 2042 106.9 Efaw AA Stillwater-Efaw, OK 1999 3247 1846 56.8 Experiment 502 Lahoma, OK 1999 2822 5426 192.3 Experiment 801 Haskell, OK 1999 1985 1916 96.5 __________________________________________________________________________________ † predicted mean grain yield using exponential model of yield on EY reported in Figure 3 §S*N, row spacing by N rate experiment N*P, N rate by P rate experiment
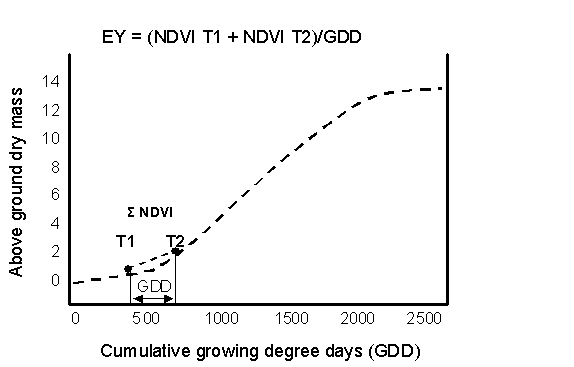
Figure 1. Schematic relationship (Rickman et al., 1996) between above ground dry
mas (estimated using NDVI) obtained at two stages of growth (T1 and T2), and
cumulative growing degree days (GDD), and the calculation of in-season estimated
yield (EY).
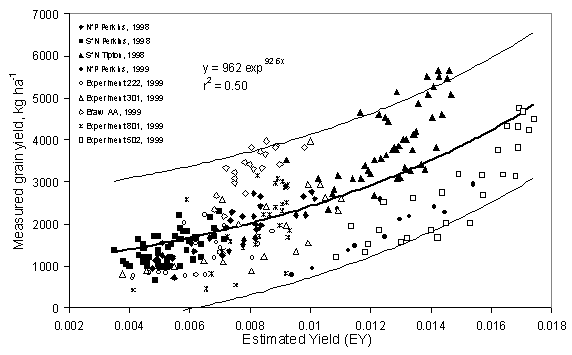
Figure 2. Relationship between in-season estimated grain yield (EY) computed
from two post-dormancy NDVI readings, divided by the cumulative growing degree
days (from Time-1 to Time-2), and measured grain yield in nine winter wheat
experiments, 1998 and 1999 (confidence limits for point estimates about the
exponential model).
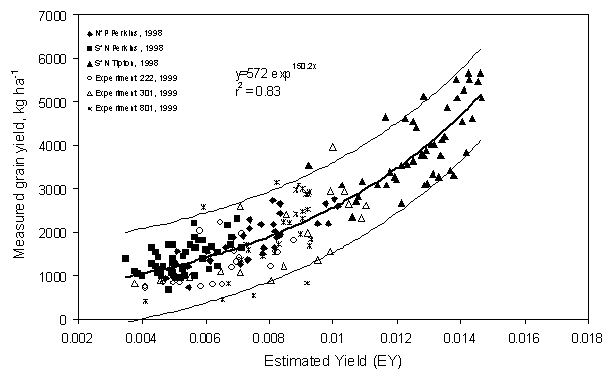
Figure 3. Relationship between in-season estimated grain yield (EY) computed
from two post-dormancy NDVI readings, divided by the cumulative growing degree
days (from Time-1 to Time-2), and measured grain yield in six of nine winter
wheat experiments, 1998 and 1999 (confidence limits for point estimates about
the exponential model).