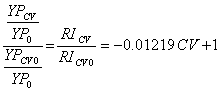ABSTRACT

Nitrogen fertilization for cereal crop production does not follow any kind of generalized methodology that guarantees maximum nitrogen use efficiency (NUE).  The objective of this work was to amalgamate some of the current concepts for N management in cereal production into an applied algorithm.  Our work at Oklahoma State University from 1992 to present has focused primarily on the use of optical sensors in red and near infrared bands for predicting yield, and using that information in an algorithm to estimate fertilizer requirements.  The current algorithm, “WheatN.1.0”, may be separated into several discreet components: 1) mid-season prediction of grain yield, determined by dividing the normalized difference vegetative index (NDVI) by the number of days from planting to sensing (estimate of biomass produced per day on the specific date when sensor readings are collected); 2) estimating temporally dependent responsiveness to applied N by  placing non-N-limiting strips in production fields each year, and comparing these to the farmer practice (response index); and 3) determining the spatial variability within each 0.4m² area using the coefficient of variation (CV) from NDVI readings.  These components are then integrated into a functional algorithm to estimate application rate whereby N removal is estimated based on the predicted yield potential for each 0.4m² area and adjusted for the seasonally dependent responsiveness to applied N.   This work shows that yield potential prediction equations for winter wheat can be reliably established with only 2-years of field data.  Furthermore, basing mid-season N fertilizer rates on predicted yield potential and a response index can increase NUE by over 15% in winter wheat when compared to conventional methods.  Using our optical sensor based algorithm that employs yield prediction and N responsiveness by location (0.4m² resolution) can increase yields and decrease environmental contamination due to excessive N fertilization. 
 

INTRODUCTION

From the early 1950’s to the early 1970’s, increased food production was a priority in agricultural areas around the world (1).  During this time period, the largest increase in the use of agricultural inputs was for nitrogen (N) fertilizer, because it had the largest impact on yield.  Since the early 1960’s, the increase in fertilizer N consumption has continued, becoming somewhat stable over the past 10 years.  Although fertilizer N consumption and cereal grain production have both increased over the last 5 decades, contamination of surface and groundwater supplies continues because the efficiency at which fertilizer N is used in grain production has remained at a stagnant 33% worldwide (2).  While only 33% of the nitrogen applied in fertilizer is recovered in the cereal grain harvest, few published reports have documented practices which significantly improve the efficiency at which N is used in cereal production.

Voss (3) noted that the greatest recent improvement in fertilizer recommendations in many states was the calibration of a soil nitrate test on which to base fertilizer N recommendations for corn (Zea mays L.).  Makowski and Wallach (4) showed that models including end-of-winter mineral soil N gave more profitable N fertilizer recommendations, but that 10 site-years of data were required for model parameter estimation.  It should be noted that wide spread adoption of soil testing remains limited in both the developed and developing world.  In Oklahoma, annual soil testing takes place on less than 10% of the agricultural land, and this number is significantly less in the developing world (Hailin Zhang, Head of OSU Soil Testing Lab, personal communication, August 2003).

Various researchers have worked to predict N mineralized from soil organic matter which could lead to improved N fertilizer recommendations (5).  Recent work by Mulvaney et al. (6) found that the concentration of amino sugar N was highly correlated with check-plot yields and fertilizer N response.  Amino sugar N was determined on 5 gram soil samples treated with 20 ml of 6M HCl heated under reflux (110-120°C) for 12 hours.  The hydrolysis mixture was then filtered and stored at 5°C.  Neutralized (use of 1 M NaOH until a pH of 6.5 to 6.8 was achieved) hydrolysates were analyzed for hydrolysable N, NH₄-N and amino sugar N using the diffusion methods described by Mulvaney and Khan (7).  This methodology successfully partitioned N-responsive from non N- responsive corn for sites that received “normal rainfall”.  It is not clear how this technique could be implemented for within-season N fertilizer recommendations, because N availability is strongly influenced by temporal changes.

Current strategies for winter wheat in Oklahoma recommend that farmers apply 33 kg N ha^-1 for every 1 Mg of anticipated wheat yield (2 lb N ac^-1 for every bushel of expected wheat grain yield) they hope to produce, subtracting the amount of NO₃-N in the surface (0-15 cm) soil profile (8).  When grain yield goals are applied using this strategy, the risk of predicting the environment (good or bad year) is placed on the producer, especially when farmers take the risk of applying all N preplant.  Schmitt et al. (9) reported similar recommendations of 20 kg N ha^-1 for every 1 Mg of corn (1.2 lb N ac^-1 for every bushel of corn) minus soil test NO₃-N and/or any credits from previous leguminous crops in the rotation.  To some extent, university extension (e.g., soil testing), fertilizer dealers, and private consulting organizations have historically used grain yield goals, due to the lack of a better alternative, and because producers have been able to relate to an input/output strategy for computing N requirements.

Many researchers have used measurements of NO₃-N in plant tissue to identify N sufficiency or deficiency at early growth stages in winter wheat (10).  However, the utility of this approach was limited since critical tissue NO₃-N levels varied as a function of temporal variability (11).  Even so, petiole NO₃-N has been successfully used in potatoes, where monitoring NO₃-N late in the season provided a mechanism for improving quality in a region where irrigation was used and temporal variability was limited (12). 

Vaughan et al. (13) applied a combination of improved spring fertilizer recommendations in winter wheat by using both total N in wheat plant tissue and soil NH₄-N to improve spring N fertilizer recommendations in winter wheat and was able to prevent over fertilization.  Work in Pennsylvania by Fox et al. (14) found that stalk NO₃-N test taken two weeks after corn had reached physiological maturity was an excellent indicator of corn N status.  A critical level of 250 mg kg^-1 separated N-sufficient from N-deficient sites.  This same work showed that chlorophyll meter readings at one-fourth milk line growth stage could be used as a good indicator of corn N status, but was less reliable if drought-stressed sites were included.  In Nebraska, Varvel et al. (15) found that chlorophyll meter readings and end-of-season stalk NO₃-N concentrations (threshold of 2000 mg kg^-1) provided additional criteria to help partition and separate fields into areas with potentially different levels of residual soil N. They proposed that this information could be used to guide soil sampling and to develop or improve site- specific N fertilizer recommendations, which should decrease environmental risk by reducing the amount of NO₃-N available for leaching.  Further inspection of the Nebraska data showed that any time stalk nitrate levels were in the 250 mg kg^-1 region (retro evaluation versus the Fox et al., 2001 data), grain yields were less than maximum (Gary Varvel, personal communication, July 2003).

Wood et al. (16) found that tissue N concentration at V10 and mid-silk were good predictors of corn grain yield, noting that field chlorophyll measurements using a SPAD-502 chlorophyll meter (Minolta Camera Co., Ltd., Japan) were highly correlated with tissue N concentrations at both of these growth stages.  Sensor work by Blackmer et al. (17) indicated that the measurement of light reflectance near 550 nm had promise as a technique to detect N deficiencies in corn leaves.  Varvel et al. (18) employed chlorophyll meter readings to calculate a sufficiency index (as-needed treatment/well-fertilized treatment) whereby in-season N fertilizer applications were made when index values were below 95%.  If sufficiency index values were below 90% at the V8 growth stage in corn, maximum yields could not be achieved with in-season N fertilizer applications.  This suggested that pre-V8 N management was critical for corn. 

Fiez et al. (19) reported on the need to reduce N losses and lower N rates in winter wheat production, especially on north-facing back-slopes.  Lengnick (20) suggested that plant indicators followed changes in landscape features that influenced biomass production and N uptake.  He speculated that these changes would not be revealed by soil test analyses.  Voss (3) suggested that a regional research approach using current and potential precision agriculture technology could provide a large and up-to-date data base on which to base nutrient recommendations across a wide spectrum of soils and crops.  This work further noted the importance of simultaneously using soil and plant productivity indicators to make site specific crop production decisions.  The resolution at which these existed was not addressed. 

Raun et al. (21) showed that yield potential could be estimated from mid-season sensor reflectance measurements (Feekes 4 to 6) in winter wheat.  Their work employed the normalized difference vegetative index (NDVI) computed from red and near infrared reflectance values [NDVI = (NIR-Red)/(NIR+Red)].  NIR and Red are the reflectance measurements in the near infrared and red bands, respectively.  This work predicted yield using the sum of two post dormancy sensor readings (NDVI) divided by the cumulative growing degree-days or GDD ((Tmin + Tmax)/2-4.4°C) from the first to the second readings.  Tmin and Tmax are the minimum and maximum temperatures in a 24 hour period.  Their index, in-season estimated yield, or INSEY was later modified whereby a single NDVI measurement was divided by the number of days from planting to sensing, counting only those days where GDD > 0 (22).  This method eliminated those days where growth was not possible as a function of temperature, regardless of the soil moisture conditions.  Raun et al. (22) showed that N fertilization based on mid-season estimates of yield potential increased NUE by more than 15% when compared to traditional practices which applied N at uniform rates.  A significant key to the success of this work was collecting sensor readings from each 1m² area and fertilizing each 1m², recognizing that the differences in yield potential and subsequent fertilizer need exists at this spatial scale.  This spatial scale was determined in earlier work, where extensive soil sampling, optical sensor measurements of plants, and geostatistical analyses, showed that significant differences in N availability existed at a 1m² spatial resolution and that each square meter needed to be treated independently to maximize benefits (23, 24).  Earlier work by Solie et al. (25) noted that the fundamental field element for sensing and treating fertility differences is that area which provides the most precise measure of the available nutrient where the level of that nutrient changes with distance.

 Taylor et al. (26) evaluated the relationship between the coefficient of variation (CV) from grain yields and plot size.  This work showed that CV’s decreased with corresponding decreases in plot sizes.  This research suggested that the small plot sizes were consistent with the resolution where detectable differences in soil test parameters existed and should be treated independently.  Research conducted at the International Maize and Wheat Improvement Center (CIMMYT) suggested that the use of within row CV’s in corn could be used to detect the physiological growth stage when expressed spatial variability was the greatest from readings collected on a daily basis throughout the growth cycle (27).

Over an eleven-year period, the authors have developed a process to determine N fertilizer application rate from optically sensed reflectance measurements that vary temporally and spatially.  The objective of this paper is to describe and justify that process.

MID-SEASON NITROGEN FERTILIZATION ALGORITHM

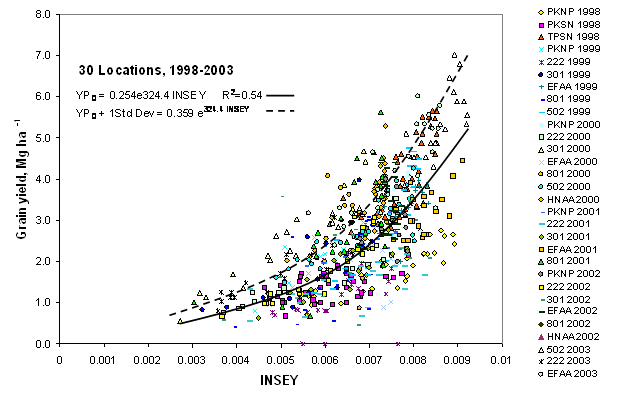
Rationale for Basing Algorithm on Predicted Yield

In the last century, yield goals have provided one of the more reliable methods for determining pre-plant fertilizer N rates in cereal production. The logic of this approach makes sense, since at any given level of yield for a specific crop, nutrient removal can be estimated based on known concentrations in each respective grain.  For example, total N concentrations in wheat, corn, and rice grain average 2.13, 1.26, and 1.23 %N, respectively (28).  Although there are expected differences in varieties/hybrids and growing conditions, these can be accurately estimated for selected production regions and cultivars.  Once expected removal amounts are known (based on a projected yield), mid-season application rates are determined by dividing removal by the projected use efficiency.  Similarly, known quantities of P, K, S, and other micronutrients within particular cereal grain crops have been published by the Potash Phosphate Institute (Norcross, GA) (29), and based on these concentrations, mid-season nutrient rates could be determined at specific foliar nutrient application efficiencies.

Johnson (30) suggested that it is usually advantageous to set the grain yield goal above that of average yields in order to take advantage of above-average growing conditions when they are encountered in dryland agriculture.  Dahnke et al. (31) reported that yield goal was the “yield per acre you hope to grow,” clearly delineating the risk farmers take when applying preplant N.  Work by Rehm and Schmitt (32) suggested that with favorable soil moisture at planting it would be smart to aim for a 10 to 20% increase over the recent average when selecting a grain yield goal. They also indicated that if soil moisture was limiting, yield goals based on past averages were not advisable for the upcoming crop.  This is an important observation, since the strategy proposed in this paper could theoretically adjust mid-season projected yield goal or yield potential based on soil profile moisture at planting, or better yet, profile moisture at the time of sensing.  This is consistent with observations by Black and Bauer (33) who noted that grain yield goal should be based on how much water was available to the winter wheat crop from stored soil water to a depth of 1.5 m in the spring plus the anticipated amount of growing season precipitation.

Oklahoma State University Procedure and Algorithm for Calculating Spatial and Temporal Varying N Fertilizer Rates

The Oklahoma State University optical sensor based algorithm calculates N fertilizer rates, and it depends on making an in-season estimate of the potential or predicted yield, determining the likely yield response to additional nitrogen fertilizer, and finally calculating N required to obtain that additional yield.  In addition, a procedure has been developed to modify the calculated fertilizer response to account for the effect of spatial variation as it affects the crop’s ability to respond to additional fertilizer.  Our approach is based on the ability to predict yield potential and to calculate N required based on the total amount of a given nutrient that will be removed in each crop.

 

1. Estimate of Yield Potential

Work by Stone et al. (34) showed that early-season NDVI readings of winter wheat measured with an optical sensor were highly correlated with total above ground plant biomass.  The effect of the number of days of active plant growth prior to sensing was minimized by dividing NDVI readings by the number of days from planting to sensing where GDD > 0.  Including only those days where GDD was more than 0 was necessary in order to remove days where growth was not possible in winter wheat, and which were notably variable over sites and years.  In essence, the index, INSEY, was an estimate of biomass produced per day when growth was possible.  Raun et al. (22) showed that optical sensor readings could be collected once, anytime between Feekes growth stages 4 and 6, and that INSEY was an excellent predictor of yield (grain or forage depending on the system).  This work was recently updated to include 30 locations over a 6-year period from 1998 to 2003 (Figure 1). 

What is striking from this research is that planting dates ranged from September 24 to December 1 (difference of 68 days), and sensing dates ranged from February 10 to April 23 (difference of 72 days), (range of differences from planting to sensing of 133 to 184 days) yet yield prediction remained quite good (solid line).  The results clearly indicated that, for winter wheat, biomass produced per day was an excellent predictor of grain yield.  Furthermore, over this 6-year period, 5 different varieties (Tonkawa, 2163, Custer, 2137, and Jagger) were included in this database (Table 1).  In this regard, it was noteworthy to find such a good relationship with final grain yield, because so many uncontrolled variables from planting to sensing (rainfall, planting date, temperature, etc.) had the potential to adversely affect this relationship.  The good correlation was somewhat surprising when considering the many post-sensing stresses that could be encountered, and would decrease yields (rust, drought, weed infestations, etc.).  These unpredictable by-site problems would undoubtedly decrease correlation, since all experimental sites were included in the database.  Furthermore, considering the many post sensing conditions that could impact the relationship between INSEY and final grain yield, the relatively good fit of the exponential curve in Figure 1 (solid line) strongly supports the argument that yield potential can indeed be predicted.  However, that potential may not be realized because post-sensing conditions could adversely impact final grain yield.

Because of the importance of yield potential for determining N application rates, we must expand the concept.  The yield potential for any given 0.4m² area is the grain yield achievable, considering total plant growth from planting, accounting for plant stand and/or damage on the date of sensing.  The same spot will likely have the same yield potential whether or not it was sensed on March 1, or March 10 for a given year, since days from planting acts as the normalized divisor.  The relationship between yield data and sensor data can be described by an exponential curve.  However, standard regression techniques produce a prediction model that includes data from fields whose yields were adversely affected by events subsequent to the date of sensing that could not be predicted.  Consequently, a model of actual grain yield will under predict or over predict potential grain yield at the sensing date.  To correctly predict the potential yield, the model should be fitted to yields unaffected by adverse conditions from sensing to maturity.  Since actual yields include some that were reduced by poor growing conditions after sensing, and some that were not, it is important to use the actual yields unaffected by post sensing factors when predicting potential yield.    

There is currently no established empirical method to determine how much the curve should be shifted.  We have elected to adjust the constant ‘a’ within the exponential model (y = ae^bx) such that the number of observations above the curve was 32% of the total data points (Figure 1.).  This curve more realistically represents the yield potential achievable in rainfed winter wheat considering that post-sensing stresses (moisture, disease, etc.) from February to July could lower “observed yields.”  Thus, yield potential or YP₀ + 1 standard deviation is currently used in our algorithm for predicting yield potential.  The model currently used to predict wheat grain yield is: 

                                                                                       (1)

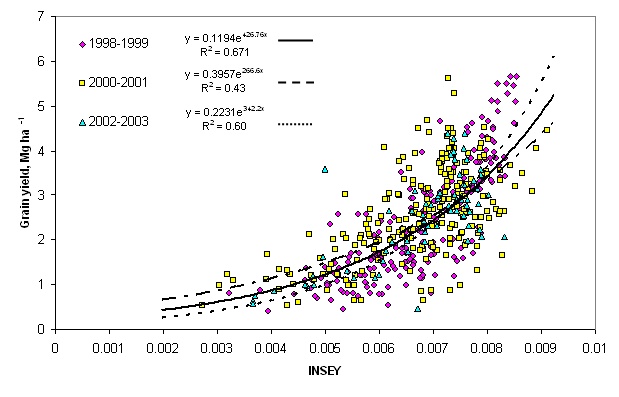
It is of further importance to note that differences from yield prediction equations formulated using the first 2 years (1998-1999, 8 locations), second 2 years (2000-2001, 12 locations), and third 2 years (2002-2003, 10 locations) of field data, did not differ substantially when compared to each other (Figure 2).  This suggests that it is possible to establish reliable yield potential prediction from only 2 years of field data, provided that enough sites were evaluated within this time period.  Regression significance (R²) differed among the 3, 2-year data sets, which was expected, but with very small differences between regression coefficients.  For all the 3, 2-year data sets, outer limits (left edge of the points from each 2-year data set moving from left to right) did not change substantially, and the equations were quite similar to that found for the 6-year model (Figures 1 and 2).
2. Estimating the Responsiveness to Applied N

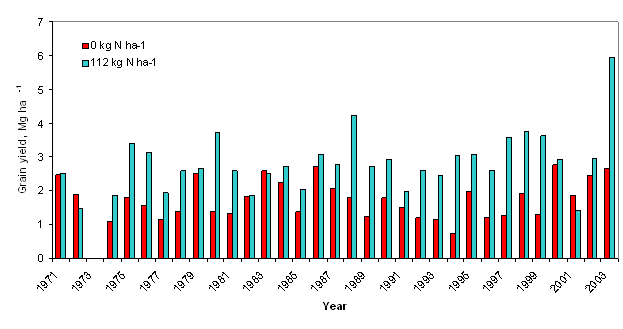
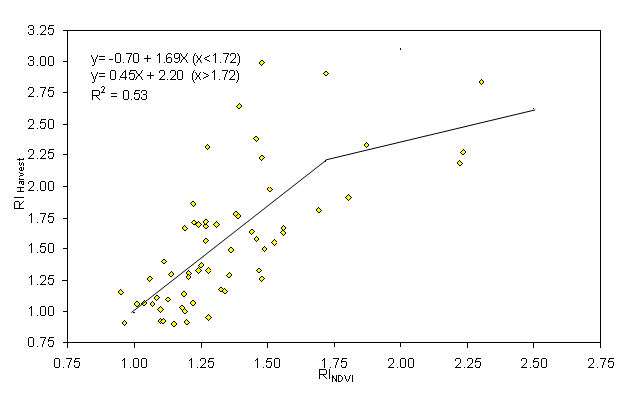
Identifying a specific yield potential does not translate directly to an N recommendation.  Determining the extent to which the crop will respond to additional N is equally important.  The concept of the response index (RI) was expanded from initial work by Johnson and Raun (35) to predict crop response to additional N fertilizer using in-season sensor measurements (36).  The Response Index is defined as:
                                                                                                     (2)
Where:             RI_Harvest is the fertilizer Response Index for a harvested crop.
                        Yld_NRich is the grain yield from an area treated within sufficient N fertilizer to
                                    assure that N is non-limiting.
                        Yld_FieldRate is the grain yield from an adjacent area treated at the normal field
                                    N application rate.
RI varied from field to field and over years and likely varied spatially within a field.  To determine RI, N fertilizer was applied to a strip extending across a field at a rate sufficient to assure that N was not limiting, but not excessive (Nitrogen Rich Strip).  Midseason estimates of RI_Harv were made by optically scanning the growing crop and calculating the NDVI response index, RI_NDVI:
                                                                                                           (3)
Where:             NDVI_NRich is NDVI of an area within the NRich strip
                        NDVI_FieldRate is NDVI of an adjacent area treated at the normal N rate.

This fertilizer index was developed following comprehensive work by Johnson and Raun (35) demonstrating that the response to applied N in the same field is entirely variable from one year to the next and independent of whether or not previous year yields were high or low.   They studied grain yield response to applied N in a long-term replicated experiment where the same rates were applied to the same plots each year for over 30 years.  The response to applied N changed drastically from one year to the next, with the check plot yield (no N applied over this 30+ year period) showing no consistent trend to decline (Figure 3).  This was attributed to N mineralization and variable N contributions from the atmosphere and rainfall that were unpredictable over time and dependent on highly variable weather conditions (35).

Because the response to N fertilizer is dependent on the supply of non-fertilizer N (mineralized from soil organic matter, deposited in the rainfall, etc.) in any given year, N management strategies that include a reliable mid-season predictor of RI should dramatically improve NUE in cereal production (35).  This paper noted that the RI values changed considerably when collected from the same plots that had been managed the same way for 30 years.  This was attributed to the striking differences in rainfall and temperature from one year to the next and associated crop need (temporal variability), which influenced how much non-fertilizer N was used by the crop. 

The relationship between RI computed from NDVI readings collected from the check plots and adequately N fertilized plots at Feekes growth stages 4 to 6 (RI_NDVI) with RI computed from harvested grain (grain yield ratio determined from the same respective plots, RI_Harv) over 63 locations from 1998 to 2003 is reported in Figure 4.  RI_NDVI was positively correlated with RI_Harvest over this 6-year period.  However, RI_NDVI could greatly underestimate the benefits of additional N fertilizer particularly in the middle range.  The improved fit of a linear-linear curve in this middle region indicated that RI_NDVI measurements in midseason could not fully account for intervening causes improving final yield.  Despite this limitation, RI_NDVI has proven to be a good, conservative predictor of wheat grain yield with additional fertilizer.

Where RI_NDVI is used to predict the average grain yield response to additional fertilizer, average NDVI of the NRich strip should be compared with average NDVI of a field rate strip immediately adjacent to the NRich strip.  Where RI_NDVI is used to predict spatially varying response within a field, NDVI measurements should be made in an area where observation indicates that response to fertilizer is high.

The highest NDVI measurement along the NRich strip can be used to calculate (Equation 1) the maximum potential yield.  YP_max is the maximum yield that could be expected within the most productive area in a field when N was not limiting for the year of measurement.

The boundaries circumscribing potential yield with and without additional fertilizer are the curves predicting potential yield without additional fertilizer (YP₀), potential yield with additional fertilizer (YP_N), the maximum expected yield and a cutoff for areas with few or no wheat plants (transition from soil to plants).  The potential yield without additional fertilizer, YP₀, can be calculated directly by equation 1.

                                                                                      (4)
The following equations predict the potential yield with additional N fertilizer, YP_N:

                                      (5a)

Or

                                                                (5b)

Observations over several years indicate that values of NDVI < 0.25 occur on bare soil or on soil with wheat stands so poor at Feekes 5 that they will not produce appreciable yields.

 

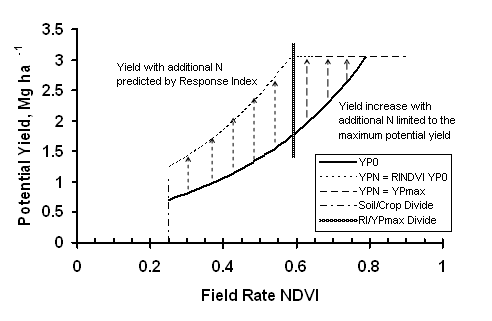
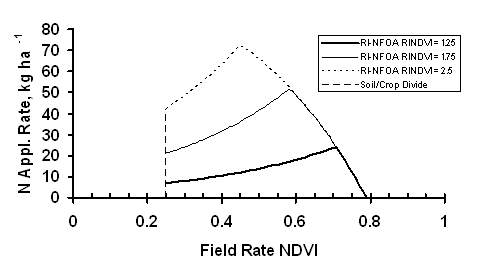
Examination of Figure 5 illustrates the critical points of the RI theory for predicting yield increase.  Below field rate NDVI = 0.25, when measured after 120 days of active plant growth, crop potential yield is considered low enough that there are no appreciable benefits in adding additional N.  This is the transition from bare soil to wheat.  In this example, between NDVI = 0.25 and NDVI = 0.57 the crop benefits from additional N, and the potential yield increase is the product of RI and potential yield without additional N, YP₀.  Between NDVI = 0.57 and NDVI = 0.73, additional fertilizer can boost grain yield up to the maximum potential yield, YP_max.  Beyond NDVI = 0.73 there is no benefit for additional fertilizer N, because potential yields have reached the maximum for the field.

The RI theory for predicting yield increase with additional N has one additional consequence.  Increasing the value of RI causes YP_N to more rapidly reach YP_max (Figure 6).  This causes the division point separating the region where the response index controls YP_N from the region where YP_max limits YP_N to shift to lower values of NDVI.  At its extreme, where RI_NDVI = 4.3, the crop yield at any location in the field and NDVI ³ 0.25 can be raised to the maximum yield.

The topdress N requirement can be calculated by:

                                                                                           (7)

Where:                                                             R is the N application rate, kg/ha

23.9 is the decimal percentage of N by weight
        contained in wheat grain multiplied by a
        conversion constant

h is an efficiency factor, 0.5 £ h £ 0.7

 

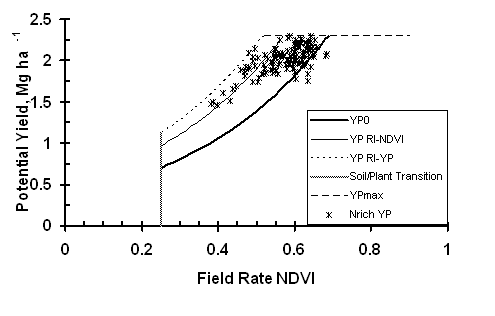
Plots of equation (7) for response indices of 1.25, 1.75, and 2.5 illustrate the effect of the RI on the nitrogen application rate (Figure 7).  The maximum N application rate for RI = 1.25 was 23.7 kg ha^-1, and the peak value did not occur until the field rate NDVI reached 0.70.  As RI increased to 2.5, the peak N application rate increased to 72.4 kg ha^-1, and the peak application rate occurred at a much lower value of field rate NDVI, 0.45.  For the conditions of YP_max = 3 Mg ha^-1 and 120 days after planting where GDD > 0, RI would equal 4.3, the N application rate equals 92.9 kg ha^-1, and the peak application rate occurs at NDVI equals 0.25.  In that case, only N is the limiting factor. 

Validation of the Oklahoma State University Optical Sensor Based Algorithm for Crop Nitrogen Fertilization occurs at two levels, paired comparisons of estimated yield from NRich and adjacent field rate fertilizer strips and an extensive series of field trials testing the algorithm.  Solie et al. (2004) (reference not included) examined 16 N Rich strips sensed with either the GreenSeeker^TM sensor or IKONIS satellite imagery.  For the IKONIS imagery, NDVI was calculated for paired pixels in the N Rich strip and the adjacent field rate area.  Pixel size was 4 by 4 m and paired data were separated by one pixel, 4 m.  An examination of the data compared with the imagery showed that aberrations in the form of spikes in RI_NDVI occurred whenever the NRich strip crossed a terrace.  These spikes occurred because of the relatively large pixel size and the fact that data pairs were separated by 4 m and NDVI values changed between the backside and channel of the terraces.  The result was no relatedness between “paired” measurements.  Data in the vicinity of terraces were deleted.  Potential yield was calculated for data from the NRich strip.  YP_NRich data were plotted in Figure 8 along with the YP₀, YP_N, YP_max and Soil/Plant transition curves as a function of field rate NDVI.  The YP_N curve was calculated using the maximum value of RI_NDVI along the strip, RI_NDVI = 1.37. 

All data fell on or below the YP_max cap, but Nrich potential yield data paired with field rate NDVI measurements ³ 0.52 were clustered closely in the vicinity of the cap.  The few measurements falling below the YP₀ boundary were a consequence of the limited relatedness that could occur when measurements separated by 4 m were use to calculate RI_NDVI.  In these instances, RI_NDVI < 1.  As noted previously, RI_NDVI provided a conservative estimate of NDVI with a number of YP_NRich data points paralleling the YP_N curve but with values greater than predicted by RI_NDVI.  To overcome the problem of underestimating potential yield, an alternative response index based on potential yield was formulated, RI_YP:

                                     (8)

A curve calculated with RI_YP = 1.58 (the greatest difference of NDVI and INSEY between data pairs) bounded all data and passed through the maximum value of YP_NDVI in the region where RI defined YP_N.  This NRich strip as well as the other 15 NRich strips, were examined by Solie et al. (2004) confirmed the theory that potential yield with additional N could be increased by the product of YP₀ measurement times the response index in the region where the response index set the boundary.  At higher levels of NDVI, all treated areas could be raised to a “cap”, YP_max.

Over the last five years, an extensive series of field trials have been conducted to test the Optical Sensor Based Algorithm for Crop Nitrogen Fertilization.  Results of these experiments have supported the validity of the theory and these have been reported at http://www.dasnr.okstate.edu/nitrogen_use.  

Adjusting RI for Reduced or Increased Response to Nitrogen

Evaluation of results testing the Optical Sensor Based Algorithm for Crop Nitrogen Fertilization and the NRich strip have shown that there are regions in the field where the response to additional N is less than or occasionally greater than predicted by the algorithm.

Measuring the variability in plant stand and growth at high resolution, less than 0.4 m², in farmer fields can enable us to adjust the response index for mid-season N fertilization in grain crops.  In general, this small area spatial variability can be estimated by the coefficient of variation (CV) of high resolution measurements of NDVI.  CV has been shown to be highly correlated with plant population within each 0.4m² area.  NDVI is well correlated with N uptake (34), and since N uptake is the product of N content and plant biomass (plant population), it follows that estimates of N uptake will be improved by identifying changes in plant population and plant growth.  Because of this relationship, we can decipher more about the potential yield obtainable with added N fertilization than by an average value of NDVI within the sensed and treated area.  If plant stands and growth are irregular (high CV), the potential yield with added N fertilization, RI, will be lower than if plant stands are uniform (low CV) with the same mean NDVI.  On-the-go monitoring of the NDVI coefficient of variation offers the potential to improve our calculation of N fertilizer rate.

The ability to accurately measure CV’s on-the-go is also a function of the sensors employed.  The sensors developed by Oklahoma State University and currently sold by NTech Industries (Ukiah, CA) collect many individual readings (>10 in each 0.4 m² traveling at 10 mph).  No other precision agricultural technology being developed today can collect as many comprehensive readings on such a small scale, and on-the-go.  Work by Taylor et al, (37) indicated that 15 to 16 readings from each area of interest were required to obtain a reliable composite soil sample.  The 10 readings collected from each 0.4 m² used here were considered to be sufficient to obtain a composite sample from such a small area, understanding that the 10 sensor readings were representative of each 0.4 m² surface area.  The resultant CV from the area of interest is representative of the variability from the same 0.4 m² area, not just a small portion as would be the case with chlorophyll meters.  Clearly, plant stands should be expected to vary at the same scale for which they are planted, which is by seed in corn.

Over the last two years, high frequency measurements of NDVI were made and wheat yields collected at 1 m² resolution (Figure 9).  These data show a definite relationship between CV within a plot and grain yield, despite the scatter in data.  An equation (Eqn. 9) relating the response index to the coefficient of variation can be derived the linear model for CV – wheat yield data:

                                                                         (9)

Dividing by the average yield at CV = 0, YP_CV0 gives:

                                                                    (10)

When measured in the field, NDVI_FldRate always has a CV > 0.  Equation 11 can be used to calculate the intercept RI_CV0:

                                                                               (11)

Where RI_Max is the maximum response index along the NRich strip and CV_MaxRI is the CV of the field rate NDVI used to calculate RI_Max. 

Predicted yield using RI_CV , YP_CV, is calculated by equation 12:

                                                                                              (12)

These equations hold for RI_NDVI, RI_YP, or any other response index predicting increased yield with additional fertilizer N.  The effect of CV on the response index is similar to that seen with changes in measured RI (Figure 10).  Although CV of wheat used to calculate YP_max is generally very low, there can be instances when yields predicted using RI_CV are greater than YP_max. 

DISCUSSION

If the resolution where significant differences in biological properties (plant or soil) were found at 0.4 m², that same resolution would be where recognizable differences in statistical properties could be discerned as well.  Nutrients can vary at different scales for different reasons.  Variability at the finest scale encompasses all causes.  At coarser scales, we average out some of the cause for variability.  Spatial variability of soil nutrients has already been established for a resolution scale of 0.4m².  Therefore, variability among 0.4m² areas is a function of nutrient availability, whereas variability within 0.4m² is likely a function of crop conditions other than nutrient availability.  Furthermore, it should be noted that plants and their roots integrate nutrient variability that can exist within each 0.4m², but that is not expressed because plant uptake and/or growth will average whatever variability might be present at that scale.

Although CV’s from small yield potential plots assisted in removing some of the variation in predicted yield when combined with INSEY (in season estimated yield), this approach is flawed since the CV needs to be applied to the response index for added N fertilization.  Adjusting RI as a function of CV can account for the inability to reach the yield predicted by RI or maximum potential yield,YP_max.  

The yield potential obtainable without added N fertilization (YP₀) for a minimum sized field element should be independent of CV.  This was confirmed when evaluating the relationship between CV determined from NDVI readings taken between Feekes 4 and 6 over 21 locations from 2000 to 2003, and where yield data were also collected from 1m² areas (Figure 6).  Although there was a trend for grain yields to decrease with increasing CV, correlation was poor. 

Unlike YP₀, the yield potential obtainable with added N fertilization (YP_N) should be dependent on CV.  While actual yield level with no added inputs is independent of CV, the yield level that can be achieved if changes or additions are made is directly related to how much the level of variability existed within each 0.4m² area.  When CV is low, a responsive field element should be capable of greater yield than when a similarly responsive field element CV is large.  To test this concept, observed grain yield obtained when added N fertilization occurred after sensing was evaluated as a function of predicted yield using INSEY and the coefficient of variation at the time of sensing in the equation (YP_N_CV).  Predictive methods for determining YP_N_CV were delineated in the previous section.  For all the plots reported in Figure 7, NDVI sensor readings were taken from winter wheat somewhere between Feekes growth stages 4 and 6.  Enough readings were collected from each plot to determine the CV.  Following sensor readings, N was applied at different rates (varied by location and year) to achieve the yield potential estimated in the RI-NFOA algorithm.  CV data were not used to determine N application rates.  To evaluate the potential usefulness of CV for predicting the yield that could be achieved with added N fertilization, actual yield, YP_N and YP_N_CV were plotted for all 6 trials where these data were collected (Figure 11).  YP_N clearly resulted in overestimating actual yields obtained, 5.5 Mg ha^-1.  YP_N_CV values more closely followed observed yield.  When actual INSEY values exceed 0.006, observed yield clearly reached a plateau or yield maximum of 3.0 Mg ha^-1.  Although the current YP_N_CV formula employed resulted in a plateau at somewhat higher INSEY values (0.008) than with observed yield (0.006), it predicted a yield plateau. 

The need to sense biological properties on a small scale (0.4m² or smaller) was established by Solie et al. (24).  Not until recently did we consider the evaluation of statistical properties within each 0.4m², understanding that the variability within each 0.4m² would be associated with something other than nutrient variability that would be minimal at this scale.  Fortunately, the sensors developed and used in all the Oklahoma State University Sensor research are capable of collecting enough data within each 0.4m² to calculate meaningful statistical estimates at this small scale.  Now, these statistical estimates on each 0.4m² can be combined with average NDVI from the same 0.4m² to better predict mid-season yield and subsequent fertilizer N rate requirements.  Using the RI-NFOA algorithm reported earlier, Raun et al. (22) showed that winter wheat NUE was improved by more than 15% when N fertilization was based on INSEY calculated from optically sensed NDVI, determined for each 1m² area, and the response index when compared to traditional practices at uniform N rates.  We are not aware of any biological basis to suggest that this approach would not be suitable in other cereal crops.

References

1. Johnston, A.E. Efficient use of nutrients in agricultural production systems. Commun. Soil Sci. Plant Anal. 2000, 31, 1599-1620.

2. Raun, W.R.; Johnson, G.V. Improving nitrogen use efficiency for cereal production. Agron. J. 1999, 91, 357-363.

3. Voss, R. Fertility recommendations: past and present. Commun. Soil Sci. Plant Anal. 1998, 29, 1429-1440.

4. Makowski, D.; Wallach, D. How to improve model-based decision rules for nitrogen fertilization. Eur. J. Agron. 2001, 15, 197-208.

5. Cabrera, M.L.; Kissel, D.E. Evaluation of a method to predict nitrogen mineralized from soil organic matter under field conditions.  Soil Sci. Soc. Am. J. 1988, 52, 1027-1031.

6. Mulvaney, R.L.; Khan, S.A.; Hoeft, R.G.; Brown, H.M. A soil organic nitrogen fraction that reduces the need for nitrogen fertilization. Soil Sci. Soc. Am. J. 2001, 65, 1164-1172 

7. Mulvaney, R.L.; Khan, S.A. Diffusion methods to determine different forms of nitrogen in soil hydrolysates.  Soil Sci. Soc. Am. J. 2001, 65, 1284-1292.

8. Johnson, G.V.; Raun, W.R.; Zhang, H.; Hattey, J.A. Soil fertility handbook; Okla. Agric. Exp. Sta.: Stillwater, OK, 2000; 61-64.

9. Schmitt, M.A.; Randall, G.W.; Rehm, G.W. A soil nitrogen test option for N recommendations with corn. Univ. of Minnesota Ext. Serv; 1998; FO-06514-GO.

10. Vaughan, B.; Barbarick, K.A.; Westfall, D.G.; Chapman, P.L. Tissue nitrogen levels for dryland hard red winter wheat.  Agron. J. 1990, 82, 561-565.

11. Raun, W.R.; Westerman, R.L. Nitrate-N and phosphate-P concentration in winter wheat at varying growth stages. J. Plant Nutr. 1991, 14, 267-281.

12. Zhang, H.; Smeal, D.; Arnold, R.N.; Gregory, E.J. Potato nitrogen management by monitoring petiole nitrate level. J. Plant Nutr. 1996, 19, 1405-1412.

13. Vaughan, B.; Westfall, D.G.; Barbarick, K.A.; Chapman, P.L.  Spring nitrogen fertilizer recommendation models for dryland hard red winter wheat.  Agron. J. 1990, 82, 565-571.

14. Fox, Richard H.; Piekielek, William P.; Macneal Kirsten E. Comparison of late-season diagnostic tests for predicting nitrogen status of corn.  Agron. J. 2001, 93, 590-597.

15. Varvel, G.E.; Schepers, J.S.; Francis, D.D. Chlorophyll meter and stalk nitrate techniques as complementary indices for residual nitrogen.  J. Prod. Agric. 1997, 10, 147-151.

16. Wood, C.W.; Reeves, D.W.; Duffield, R.R.; Edmisten, K.L. Field chlorophyll measurements for evaluation of corn nitrogen status.  J. Plant Nutr. 1992, 15, 487-500 

17. Blackmer, T.M.; Schepers, J. S.; Varvel, G.E. Light reflectance compared with other nitrogen stress measurements in corn leaves. Agron J. 1994, 86, 934-938.

18. Varvel, Gary E.; Schepers, James S.; Francis, Dennis D. Ability for in-season correction of nitrogen deficiency in corn using chlorophyll meters.  Soil Sci. Soc. Am. J. 1997, 61, 1233-1239 

19. Fiez, T.E.; Pan, W.L.; Miller, B.C. Nitrogen use efficiency of winter wheat among landscape positions.  Soil Sci. Soc. Am. J. 1995, 59, 1666-1671.

20. Lengnick, L.L. Spatial variation of early season nitrogen availability indicators in corn. Commun. Soil Sci. Plant Anal. 1997, 28, 1721-1736.

21. Raun, W.R.; Johnson, G.V.; Stone, M.L.; Solie, J.B.; Lukina, E.V.; Thomason, W.E.; Schepers, J.S. In-season prediction of potential grain yield in winter wheat using canopy reflectance. Agron. J. 2001, 93, 131-138 

22. Raun, W.R.; Solie, J.B.; Johnson, G.V.; Stone, M.L.; Mullen, R.W.; Freeman, K.W.; Thomason, W.E.; Lukina, E.V. Improving nitrogen use efficiency in cereal grain production with optical sensing and variable rate application. Agron. J. 2002, 94, 815-820.

23. Raun, W.R.; Solie, J.B.; Johnson, G.V.; Stone, M.L.; Whitney, R.W.; Lees, H.L.; Sembiring, H.; Phillips, S.B. Micro-variability in soil test, plant nutrient, and yield parameters in bermudagrass. Soil Sci. Soc. Am. J. 1998, 62, 683-690.

24. Solie, J.B.; Raun, W.R.; Stone, M.L. Submeter spatial variability of selected soil and bermudagrass production variables. Soil Sci. Soc. Am. J. 1999, 63, 1724-1733.

25. Solie, J.B.; Raun, W.R.; Whitney, R.W.; Stone, M.L.; Ringer, J.D. Optical sensor based field element size and sensing strategy for nitrogen application. Trans. ASAE 1996, 39 (6), 1983-1992

26. Taylor, S.L.; Payton, M.E.; Raun, W.R. Relationship between mean yield, coefficient of variation, mean square error and plot size in wheat field experiments. Commun. Soil Sci. Plant Anal. 1999, 30, 1439-1447.

27. Raun, W.R.; Solie, J.B.; Freeman, K.W.; Stone, M.L.; Martin, K.L.; Johnson, G.V.; Mullen, R.W. Growth stage, development, and spatial variability in corn evaluated using optical sensor readings. J. Plant Nutr. 2003, (in press).

28. Tkachuk, R. 1977. Calculation of the nitrogen-to-protein conversion factor; In Nutritional standards and methods of evaluation for food legume breeders; Hulse, J.H., K.O. Rachie Billingsley, L.W; International Development Research Centre: Ottawa, 1977; 78-82.

29. Potash Phosphate Institute.  Plant food uptake for Great Plains Crops. Norcross, GA.

30. Johnson, G.V. General model for predicting crop response to fertilizer. Agron. J. 1991, 83, 367-373.

31. Dahnke, W.C.; Swenson, L.J.; Goos, R.J.; Leholm, A.G. Choosing a crop yield goal. North Dakota State Ext. Serv., Fargo, North Dakota. 1988; SF-822.

32. Rehm, George; Schmitt, Michael. Setting realistic crop yield goals. Minnesota Ext. Serv., Univ. of Minnesota, 55108. 1989; AG-FS-3873.

33. Black, A.L.; Bauer, A. Setting winter wheat yield goals. In J.L. Havlin (ed.), Central Great Plains Profitable Wheat Management Workshop Proc., Wichita, KS., Aug. 17-20, 1988; Potash & Phosphate Institute, Atlanta, GA.

34. Stone, M.L.; Solie, J.B.; Raun, W.R.; Whitney, R.W.; Taylor, S.L.; Ringer, J.D. Use of spectral radiance for correcting in-season fertilizer nitrogen deficiencies in winter wheat. Trans. ASAE 1996, 39 (5), 1623-1631.

35. Johnson, G.V.; Raun, W.R. Nitrogen response index as a guide to fertilizer management. J. Plant Nutr. 2003, 26, 249-262.

36. Mullen, R.W.; Freeman, Kyle W.; Raun, William R.; Johnson, G.V.; Stone, M.L.; Solie, J.B. Identifying an in-season response index and the potential to increase wheat yield with nitrogen.  Agron. J. 2003, 95, 347-351.

37. Taylor, S.L.; Johnson, G.V.; Raun, W.R. A field exercise to acquaint students with soil testing as a measure of soil fertility status and field variability. J. Nat. Resour. Life Sci. Educ. 1997, 26, 132-135.

Table 1.  Summary of planting, sensing, and harvest dates over 30 locations and 6 years.

Experiment	Crop Cycle	Planting Date	Sensing Date	Harvest Date	Variety
Perkins N*P	1997-98	Oct-21-97	Apr-02-98	Jun-16-98	Tonkawa
Perkins S*N	1997-98	Oct-21-97	Apr-02-98	Jun-16-98	Tonkawa
Tipton S*N	1997-98	Oct-10-97	Mar-01-98	Jun-03-98	Tonkawa
Perkins N*P	1998-99	Oct-12-98	Mar-04-99	Jun-09-99	Tonkawa
Stillwater 222	1998-99	Oct-13-98	Feb-24-99	Jun-15-99	Tonkawa
Efaw 301	1998-99	Oct-15-98	Mar-24-99	Jun-15-99	Tonkawa
Efaw AA	1998-99	Nov-9-98	Mar-24-99	Jun-15-99	Tonkawa
Haskell 801	1998-99	Oct-16-98	Mar-23-99	Jun-07-99	2163
Lahoma 502	1998-99	Oct-09-98	Mar-05-99	Jun-30-99	Tonkawa
Perkins N*P	1999-00	Oct-08-99	Feb-08-00	May-30-00	Custer
Stillwater 222	1999-00	Oct-07-99	Feb-10-00	Jul-06-00	Custer
Efaw 301	1999-00	Oct-07-99	Feb-10-00	Jun-02-00	Custer
Efaw AA	1999-00	Oct-07-99	Feb-15-00	Jul-07-00	Custer
Haskell 801	1999-00	Oct-08-99	Mar-14-00	Jun-02-00	2137
Lahoma 502	1999-00	Oct-12-99	Feb-15-00	Jun-13-00	Custer
Hennessey AA	1999-00	Oct-07-99	Feb-15-00	Jun-07-00	Custer
Perkins N*P	2000-01	Nov-17-00	Apr-13-01	Jun-07-01	Custer
Stillwater 222	2000-01	Nov-20-00	Apr-13-01	Jun-12-01	Custer
Efaw 301	2000-01	Nov-16-00	Apr-13-01	Jun-11-01	Custer
Efaw AA	2000-01	Nov-22-00	Apr-23-01	Jun-11-01	Custer
Haskell 801	2000-01	Oct-10-00	Apr-12-01	Jun-06-01	2137
Lahoma 502	2000-01	Dec-01-00	Apr-13-01	Jun-15-01	Custer
Perkins N*P	2001-02	Oct-16-01	Feb-27-02	Jun-11-02	Custer
Stillwater 222	2001-02	Oct-01-01	Feb-27-02	Jun-03-02	Custer
Efaw AA	2001-02	Oct-04-01	Feb-27-02	Jun-28-02	Custer
Haskell 801	2001-02	Oct-19-01	Mar-13-02	Jun-19-02	2137
Hennessey AA	2001-02	Oct-30-01	Mar-26-02	Jun-12-02	Custer
Stillwater 222	2002-03	Oct-14-02	Mar-12-03	Jun-23-03	Custer
Efaw AA	2002-03	Oct-05-03	Mar-10-03	Jun-23-03	Custer
Lahoma 502	2002-03	Sept-24-03	Feb-18-03	Jun-17-03	Custer