
Analysis of yield variability in winter wheat due to temporal variability, and nitrogen, and phosphorus fertilization
ABSTRACT
Field average based recommendations have been a common practice for recommending the major crop nutrients N and P. The problem is yield will not be the same from year to year with application of the same amount of recommended rate of fertilizer. The objectives of this study were to evaluate the effect of N and P on winter wheat grain yield and assess the effect of temporal variability on wheat grain yield. Twelve factorial combinations of four N (0, 56, 112, and 168 kg ha-1) and three P (0, 14.5, and 29 kg P ha-1) rates were evaluated in a randomized complete block design with three replications at Perkins, Oklahoma. A ten-predictor variable multiple linear regression model with two quantitative variables and their interaction (N, P and NxP) and seven indicator variables (i.e. one indicator variable for each year) was evaluated and a reduced model containing six variables was generated. Wheat grain yield responded to N rates in five of seven years. Wheat grain yield increased linearly with increase in N rates in the first two years of the study. Maximum grain yield occurred between 56 and 112 kg N ha-1. Wheat only responded to P during the first two years of the study. The reduced model revealed that most of the variability in grain yield was accounted for by five individual indicator years and N only. High variability across years in grain yield and fertilizer (N and P) response, even between years of similar grain yield, is an indication of a given season’s production dependence on factors other than N and P. This evidence has great impact for those recommendations based on yield goal as increased year-to-year yield variability with continuous cropping increases the difficulty to accurately estimate yield goals.
The need for nitrogen (N) and phosphorus (P) fertilization in crop production is well documented (Campbell et al., 1995). The search for optimum rates of these nutrients from different sources is not yet uncovered and is still a subject of research. Nelson (1990) reported that in U.S. about 30 to 50% of crop yield obtained is attributed to application of the major nutrients N and P. In another study, Oklahoma State University (2000) reported that when averaged over 71 years, N and P fertilizers explained 40% of wheat yield. In their report Stewart et al. (2005) indicated that in wheat, elimination of N fertilizer caused a reduction of at least 16% in grain yield on average. Nitrogen use efficiency was improved with better N fertilization procedures from very low to 35% (Fixen and West, 2002; Sharpley et al., 1999). It has been stressed from the research perspective to synchronize nutrient supply with crop demand in order to ensure optimum crop yield and quality while avoiding deleterious impacts on the environment (Cynthia et al., 2002).
Research showed that more N and P are applied than that is removed by crop harvested in the USA (Stewart et al., 2005). Nitrogen can enter ground water through leaching and also causes pollution through release of NOxs that contribute to global warming. Also a report from Wisconsin showed that nitrogen applied to sites with high soil NO3 levels resulted in 30% yield reduction (Bundy and Andraski, 2004).
Excess N and P application may not be necessarily a result of poor producer management, but rather, due to the prevailing weather conditions for a given area especially temperature and precipitation (Johnson and Raun, 2003) which determine availability and uptake of these major nutrients. For seasons where enough precipitation is obtained, it is likely to lose N from the system through leaching. Several researchers assessed the dependency of N leaching on moisture and precipitation. High temperature and humidity enhance volatilization of NH3 from both the soil and the plant (Lees et al., 2000; Kanampiu et al., 1997; Francis et al., 1993). Lees et al. (2000) reported estimated plant N loses of up to 42 kg N ha-1, and that losses increased with increasing N application. This suggests that the nutrient use efficiency of winter wheat is more a function of unpredictable weather than the actual amount of nutrient that is applied assuming normal crop growing conditions.
Different strategies have been developed to reduce these leaks and improve nitrogen use efficiency. One approach that is also used in Oklahoma is a recommendation for continuous wheat based on average yield goal, with adjustments for soil profile N content (Johnson, 1991; Bundy and Andraski, 2004; Olson et al., 1976; Scharf and Alley, 1994; Hossain et al., 2004). Field average recommendations are achieved by spatially dependent crop response experiments (Johnson, 2001). This approach evaluates only a few independent fixed variables in the analysis model to explain variability in a dependent variable. The limitation of this approach is that yield will not be the same from year to year with application of the same amount of recommended rate of fertilizer. Yield trends over several years might give a clue as to whether this is possible or not. Derby et al. (2005) concluded that yearly climatic factors should be considered when making fertilizer recommendations, among other things.
Several researchers have attempted to refine N-recommendation by incorporating both spatial and temporal variability. Flowers et al. (2004) found that in-season optimization of N rate was more important than site-specific management. According to their results a large reduction in N inputs (up to 48.6%) was attributed to in-season N rate optimization while a further reduction in N inputs (up to 19.6%) was possible through site-specific application. The authors also reported that nitrogen use efficiency was improved by site-specific N application compared with either field-specific or typical growers' practices. Their results clearly showed the significance of managing temporal variability that is a function of several factors.
Phosphorus is an immobile nutrient and is not directly related to yield level, but P must be at 100% sufficiency so as not to limit final yield. However, if it is in excess and in easily transportable form it could be a concern to surface and sub-surface waters (Sims et al., 1998; Heckrath et al., 1995). Numerous studies showed that high rates of P improved water uptake by promoting a deeper and more extensive root system (Payne et al., 1992; Rodriguez et al., 1996; Singh and Sale, 2000). The best method of determining the P fertility status of soils and thus determination of P requirement is through soil testing (Stewart, 2001). Recently researchers attempted to generate foliar recommendation for phosphorus in wheat and corn (Mosali et al., 2005; Girma et al., 2005). According to these authors, 4 kg ha-1 and 8 kg ha-1 P applied at pseudo-stem erection and 8th leaf unfolded growth stages of wheat and corn, respectively improved grain yields.
The objectives of this study were: 1) to generate recommendations for each year and 2) to assess the effect of temporal variability on winter wheat grain yield by fitting a linear model containing all the years and the fertilizers to project the contribution of each variable on grain yield.
MATERIALS AND METHODS
A long-term field experiment was initiated in 1996 at Perkins (Teller sandy loam, fine-loamy, mixed, thermic Udic Argiustoll), Oklahoma. Initial soil characteristics are reported in Table 1. Twelve factorial combinations of four N (0, 56, 112, and 168 kg ha-1) and three P (0, 14.5, and 29 kg P ha-1) levels were evaluated in a randomized complete block design with three replications. The plot size was 3.1 m x 9.1 m.
Both N and P were applied at planting using urea (46 kg N ha-1) and TSP (46 kg P2O5 ha-1), respectively. Wheat was harvested in June with a Massey Ferguson 8XP experimental combine with a yield-monitoring computer (Harvest Master™) to record grain weight and moisture levels, removing an area of 2 x 9.1 m from the center of each plot. Grain sub-samples collected for total N analysis were dried in a forced-air oven at 66oC, ground to pass a 140 mesh sieve (100 μm), and analyzed for total N content using a Carlo-Erba (Milan, Italy) NA-1500 dry combustion analyzer (Schepers et al., 1989).
Grain yield and N content data were subjected to analysis of variance (ANOVA) for each year using SAS (SAS institute, 2001). Analysis was also done to evaluate the effect of N, P, NxP and random year (environment) effect to assess the contribution of each of these three factors in the variability of grain yield. Indicator variables were then used to evaluate each year in multiple regression to assess the overall effect of N and P and each year’s effect on grain yield. These analyses were conducted in order to determine whether variability in yields was attributed to N and P or some other underlying temporal factors that influence response more than N and P applied. The multiple regression analysis conformed to a model with two quantitative variables and their interaction (N, P and NxP) and seven year indicator variables (i.e. one indicator variable for each year). One year (2001) was used as a reference group (i.e. dropped from the model) to obtain unique estimators of the regression coefficients for the rest of the indicator years. The regression equation for grain yield (GY) was:
GYi = b0 + b1Ni + b2Pi + b3NiPi + b4Y1i + b5Y2i + b6Y3i + b7Y4i + b8Y5i + b9Y6i + b10Y7i + ei
Where GYi = expected grain yield (kg ha-1) of the ith treatment mean
i = 1,2, . . . n
n= number of treatment means (= 36 in the study)
N & P are nitrogen and phosphorus
Y= 1,2, . . . 7 denote years 1998 through 2004
b0 = intercept
b1, b2, and b3 are coefficients for N, P, and NxP
b4, b5, … , B9 and B10 are regression coefficients for Y1, Y2, …, Y7, respectively
ei = Error term
The multiple regression analysis initially included all 10 components. Elimination of components exhibiting the least contribution to the regression sum of squares and being non-significant individually (p> 0.05) was accomplished using ‘Forward Stepwise Regression’ automatic model selection procedure. This procedure adds and drops each variable in the model using a t-statistic (Kutner et al., 2004; Neter et al. 1990). Ultimately only those components with significant (p<0.05) contribution to the multiple regression (contribute the most variability in the response variable grain yield) were retained in the reduced model. For the reduced model, REG procedure in SAS (SAS institute, 2001) was used to determine the partial squared correlation coefficients, PCORR1 and PCORR2 from Type I sequential sum squares and Type III partial sum-squares, respectively. The partial squared correlation coefficients were used to define the contribution of each predictor variable in the final reduced model by removing the effect of the other predictor variables on that predictor variable and the response variable (Cohen et al., 2002). This same procedure was also applied on grain N content data.
RESULTS AND DISCUSSION
Nitrogen, P and N by P Interaction
Wheat grain yield responded to N rates in five of seven years (Table 2). During the first two years, wheat grain yield increased linearly with N rates. Although only three years were statistically significant, wheat showed a quadratic response to N in five years after the first two years. Maximum response occurred between 56 and 112 kg N ha-1 (Table 2). In the Great Plains, N rates near 70 kg N ha–1 or less were generally sufficient to optimize small-grain crops yields in several continuous cropping studies when estimates of yield goals were difficult to obtain and no information on residual soil N content was available (Schlegel et al., 2005). Grain N content was affected in six of seven years. Accordingly it was linearly and positively related to N rate for all years except 2001 (Table 3).
The wheat crop seemed to benefit and respond to P only during the first two years of the study (Table 2). Beyond that, wheat showed no response and the application of P tended to depress yield of winter wheat, although this might be related to other unforeseen factors. The soil test P based recommendation in several states suggests an application of the amount that would equal the amount removed in harvested crops (Dahnke and Olson, 1990). Interestingly the experimental results support this approach due to a lack of significance to P that was independent of years. Consequently this shows that variability in years which is of course the function of several weather related factors did not have much influence on P use of the crop. According to recent studies by Mosali et al. (2005) foliar P was recommended to supplement P requirement of wheat versus continuous application of P as blanket pre-plant recommendation to correct deficiency in case crop requires P at the peak grain filling time. Similarly, P had effect on grain N content only in two instances (1999 and 2001) where a quadratic relationship was observed between grain N content and the three levels of P (Table 3).
No significant N and P interaction was observed for both grain yield and grain N content. Unlike the results obtained in this study, the form of N fertilizer and rate is known to affect the availability and uptake of P. According to Zhang et al. (2004) total P uptake was higher with NH4+-N fertilizer than with the NO3--N.
Evaluation of Grain Yield and N Content Variability Explained by N, P and Years
The type I sequential sum of square based analysis for N, P, N*P, Year, N*year and P*year predictor variables for grain yield (data not shown) suggested that year (about 82% of yield variability), N (6.6%), N*year (6.2%) and P*year (4.7%) contributed to the variability in yield when fitted to the model in that order. Alternatively, the type III partial sum-squares based model revealed the same outcome where P and N*P explained very little variability in grain yield for all sources included in the model. The model obtained from type I sequential sum-square with varying order of predictors in the model showed that year as a predictor variable tended to explain most of the variability in grain yield regardless of its position in the model. The results of the simultaneous regression of the mean wheat grain yield for the N, P and N*P treatments and the seven years (2001 as reference group), revealed that six of the 10 regression coefficients used in the model were significant. The reduced model that included the components that most contributed to yield was given by:
GY = 1910 + 3.5N - 453* 1998 - 1195*1999 + 531*2002 + 1104* 2003 + 1110* 2004
The parameter estimates, probabilities, partial squared correlation coefficients, i.e. SPCORR1 and SPCORR2 (from both type I and III sum squares, respectively) are given in Table 4. The model that included the six significant components in the multiple regression analysis explained a significant proportion of the variation in wheat grain yield (R2 =0.71). The coefficients in Table 4 showed that very large positive coefficients were associated with most of the indicator variables except years 1998 and 1999, where coefficients were large negatives. The partial squared correlation coefficients clearly indicated the strong effect of year variables on grain yield. Figure 1 also shows this variability across years. The high variability across years and dependency of final grain yield on these years is simply an indication of a given season’s production dependence on other factors other than N. This has great impact for those recommendations based on yield goal as increased year-to-year yield variability with continuous cropping poses difficulty in accurately estimating yield goals. This year-to-year variability also means it is not appropriate for farmers to fertilize a crop that does not reflect fertilizer response in the final yield. Indeed it has been the challenge of both researchers and farmers to know what is happening over a season as most of the farming practices are dictated by crop growth stage and the need to follow cropping calendar.
Research has demonstrated the use of optical sensors during the growing season to assess N stress and to estimate crop N requirements (Lukina et al., 2001; Raun et al., 2001; Raun et al., 2002; Stone et.al., 1996). This approach uses the in-season yield estimation procedure which is actually derived from growth rate of the crop. Phillips et al. (2004) and Flowers et al. (2001) used the normalized difference vegetation index (NDVI) to predict tiller density at 1 m2 resolution. Phillips et al. (2004) concluded that N fertilizer rates and grain yields resulting from using sensor-based estimates of tiller density were not different from those when using the standard practice for the Mid-Atlantic region at four out of six locations while at two of the six sites, sensor-based N recommendations were 11 kg N ha-1 lower than standard recommendations. They achieved a coefficient of determination of 67 to 99% when regressing tiller density estimated from NDVI against grain yield. Some researchers developed and implemented an alternative approach of N-fertilization called ‘balance sheet method’ (Vanotti and Bundy, 1994, Meisinger, 1984 Neeteson, 1995; Alvarez et al., 2004). This method essentially integrates crop production and soil N availability factors to some extent. This method however is short of considering N-losses, immobilized N and the amount that is not used by crop which can significantly differ in time. Derby et al. (2004) attempted to predict midseason N requirement of corn by taking into consideration weather and predicted yield.
Selection of the best model for grain N content revealed that N was the only significant component that explained a substantial portion of variability in grain N content. Phosphorus and the seven year indicator variables were excluded from the reduced model. This shows that grain N content of wheat is not affected by temporal variability as such for the soil type in this study, indicating that grain protein will not fluctuate year to year.
CONCLUSION
The results of this study conform to the current notion that ‘average based’ N and P recommendation should be avoided. Producers need to shift to alternate strategies that comply with current pressures for both competitiveness and environmental protection in agricultural production. The results of this study also suggest that fertilizer nutrient management requires consideration of various time scales. Mechanistic models that include variables that take into consideration both temporal and spatial variability need to be encouraged for crop production. Imperatively, producers also need to adopt this approach for efficient, profitable and sustainable production consistent with the altered N and P rates highly dependent on temporal conditions. Also, the results demonstrated that soil fertility research planning with predetermined fixed rates of N, P and K might not be appropriate. Instead, researchers need to adopt a ‘nutrient rich strip system’ alongside sensor based recommendation for N.
REFERENCES
Alvarez, R., H. S. Steinbach, S. M. Grigera, E. Cartier, G. Obregon, S. Torri, and R. García. 2004. The balance sheet method as a conceptual framework for nitrogen fertilization of wheat in a Pampean agroecosystem. Agron. J. 96:1050-1057.
Bundy, L.G. and T.W. Andraski. 2004. Diagnostic tests for site-specific nitrogen recommendations for winter wheat. Agron. J. 96: 608-614.
Campbell, C.A., R.J.K. Myers, and D. Curtin. 1995. Managing nitrogen for sustainable crop production. Fert. Res. 42:277-296
Cohen, J, S.. West, L.S. Aiken, and P. Cohen. 2002. Applied multiple regression/correlation analysis for the behavioral sciences, 3rd ed. Mahwah, NJ: Lawrence Erlbaum Assoc. Inc., 1200pp.
Derby, N.E., F.X.M. Casey, R.E. Knighton, and D.D. Steele. 2004. Midseason nitrogen fertility management for corn based on weather and yield prediction. Agron. J. 96:494-501.
Derby, N. E., D.D. Steele, J. Terpstra, R.E. Knighton, and F.X. M. Casey. 2005.
Interactions of nitrogen, weather, soil, and irrigation on corn yield. Agron. J. 97:1342-1351.
Dahnke, W.C., and R.A. Olson. 1990. Soil test correlation, calibration, and recommendation. p. 45–71. In R.L. Westerman (ed.) Soil testing and plant analysis. Soil Sci. Soc. Of Am., Madison, WI.
Fixen, P.E. and F.B. West. 2002. Nitrogen fertilizers: Meeting contemporary challenges. Ambio 31:169-176.
Flowers, M., R. Weisz, and R. Heiniger. 2001. Remote sensing of winter wheat tiller density for early nitrogen application decisions. Agron. J. 93:783-789.
Flowers, M., R. Weisz, R. Heiniger, D. Osmond, and C. Crozier. 2004. In-Season optimization and site-specific nitrogen management for soft red winter wheat. Agron. J. 96: 124-134.
Francis, D.D., J.S. Schepers, and M.F. Vigil. 1993. Post-anthesis nitrogen loss from corn. Agron. J. 85:659-663.
Girma, K., K. L. Martin, J. Mosali, K. W. Freeman, R. K. Teal, S. M. Moges, D. B. Arnall and W. R. Raun. 2005. Determination of optimum rate and growth stage for foliar applied phosphorus in corn. Commun. Soil Sci. Plant Anal. (in press).
Grant, C.A., G. A. Peterson, and C.A. Campbell. 2002. Nutrient considerations for diversified cropping systems in the Northern Great Plains. Agron. J. 94: 186-198.
Heckrath, G., P.C. Brookes, P.R. Poulton, and K.W.T. Goulding. 1995. Phosphorus leaching from soils containing different phosphorus concentrations in the Broadbalk experiment. J. Environ. Qual. 24:904-910.
Hossain, I., F.M. Epplin, G.W. Horn and E.G. Krenzer, Jr. 2004. Wheat Production and Management Practices used by Oklahoma Grain and Livestock Producers. Oklahoma Agricultural Experiment Station, Oklahoma State University, B-818.
Johnson, G.V. 1991. General model for predicting crop response to fertilizer. Agron. J. 83:367-373.
Johnson, G.V. and W.R. Raun. 2003. Nitrogen Response Index as a Guide to Fertilizer Management J. Plant Nutr. 26: 249-262.
Kanampiu, F.K., W.R. Raun and G.V. Johnson. 1997. Effect of nitrogen rate on plant nitrogen loss in winter wheat varieties. J. of Plant Nutr. 20:389-404.
Kutner, M.H., C.J. Nachtsheim, and J. Neter. 2004. Applied linear regression models. New York: McGraw-Hill Irwin, 701 pp.
Lees, H.L., W.R. Raun, and G.V. Johnson. 2000. Increased plant N loss with increasing nitrogen applied in winter wheat observed with 15N. J. Plant Nutr. 23:219-230.
Lukina, E.V., K.W. Freeman, K.J. Wynn, W.E. Thomason, R.W. Mullen, A.R. Klatt, G.V. Johnson, R.L. Elliott, M.L. Stone, J.B. Solie, and W.R. Raun. 2001. Nitrogen fertilization optimization algorithm based on in-season estimates of yield and plant nitrogen uptake. J. Plant Nutr. 24:885-898.
Meisinger, J.J. 1984. Evaluating plant-available nitrogen in soil-crop systems. p. 391–416. In Nitrogen in crop production. ASA, CSSA, and SSSA, Madison, WI.
Mosali, J., K. Girma, R.K. Teal, K.W. Freeman, K.L. Martin, J. W. Lawles and W. R. Raun. 2005. Effect of foliar application of phosphorus on winter wheat grain yield, phosphorus uptake and use efficiency. J. Plant Nutr. (in press).
Neeteson, J.J. 1995. Nitrogen management for intensively grown arable crops and field vegetables. p. 295–325. In Nitrogen fertilization in the environment. Marcel Dekker, New York.
Nelson, L.B. 1990. History of the U.S. fertilizer industry. Muscle Shoals, AL: Tennessee Valley Authority.
Neter, J., W. Wasserman, and M.H. Kutner. 1990. Applied linear statistical models, 3rd ed. Boston, MA: Irwin Inc.
Oklahoma State University. 2000. Soil Fertility Research highlights 2000. Stillwater, OK: Department of Plant and Soil Sciences, Oklahoma State University.
Olson, R.A., K.D. Frank, E.J. Diebert, A.F. Drier, D.H. Sander, and V.A. Johnson. 1976. Impact of residual mineral N in soil on grain protein yields of winter wheat and corn. Agron. J. 68:769-772.
Payne, W.A., M.C. Drew, L.R. Hossner, R.J. Lascano, A.B. Onken, and C.W. Wendt. 1992. Soil phosphorus availability and pearl millet water-use efficiency. Crop Sci. 32:1010-1015.
Phillips, S. B., D. A. Keahey, J. G. Warren, and G. L. Mullins. 2004. Estimating winter wheat tiller density using spectral reflectance sensors for early-spring, variable-rate nitrogen applications. Agron. J. 96:591-600.
Raun, W.R., J.B. Solie, G.V. Johnson, M.L. Stone, E.V. Lukina, W.E. Thomason, and J.S. Schepers. 2001. In-season prediction of potential grain yield in winter wheat using canopy reflectance. Agron. J. 93:131-138.
Raun, W.R., J.B. Solie, G.V. Johnson, M.L. Stone, R.W. Mullen, K.W. Freeman, W.E. Thomason, and E.V. Lukina. 2002. Improving nitrogen use efficiency in cereal grain production with optical sensing and variable rate application. Agron. J. 94:815-820.
Rodriguez, D., J. Goudriaan, M. Oyarzabal, and M.C. Pomar. 1996. Phosphorus nutrition and water stress tolerance in wheat plants. J. Plant Nutr. 19:29-39.
SAS Institute. 2001. Statistical analysis software. Version 8.2 ed. SAS Inst., Cary, NC.
Schepers, J. S., D. D. Francis, and M. T. Thompson. 1989. Simultaneous determination of total C, total N and 15N on soil and plant material. Commun. Soil Sci. Plant Anal. 20:949-959.
Schlegel, A. J., C. A. Grant, and J. L. Havlin. 2005. Challenging approaches to nitrogen fertilizer recommendations in continuous cropping systems in the Great Plains. Agron. J. 97(2):391-398.
Scharf, P.C. and M.M. Alley. 1994. Residual soil nitrogen in humid region wheat production. J. Prod. Agric. 7:81-85.
Sharpley, A.N., T. Daniel, T. Sims, J. Lemunyon, R. Stevens, and R. Parry. 1999. Agricultural phosphorus and eutrophication. Publ. 149., Washington, DC: USDA-ARS.
Sims, J.T., R.R. Simard, and B.C. Joern. 1998. Phosphorus loss in agricultural drainage: Historical perspective and current research. J. Environ. Qual. 27:277-293.
Singh, D.K. and P.W.G. Sale. 2000. Growth and potential conductivity of white clover roots in dry soil with increasing phosphorus supply and defoliation frequency. Agron. J. 92:868-874.
Stewart, W.M. 2001. Phosphorus boosts profitable
winter wheat forage and grain production. Lubbock, TX: Potash & Phosphate
Institute Ref. # 01100.
www.ppi-ppic.org
Stewart, W. M. , D. W. Dibb, A. E. Johnston, and T. J. Smyth. 2005. The
contribution of commercial fertilizer nutrients to food production. Agron. J.
97:1-6.
Stone, M.L., J.B. Solie, W.R. Raun, R.W. Whitney, S.L. Taylor, and J.D. Ringer. 1996. Use of spectral radiance for correcting in-season fertilizer nitrogen deficiencies in winter wheat. Trans. ASAE 39:1623-1631.
Vanotti, M.B. and L.G. Bundy. 1994. Corn nitrogen recommendations based on yield response data. J. Prod. Agric. 7:249-256.
Zhang, F., S. Kang, J. Zhang, R. Zhang, and F. Li. 2004. Nitrogen fertilization on uptake of soil inorganic phosphorus fractions in the wheat root zone. Soil Sci. Soc. Am. J. 68: 1890-1895.
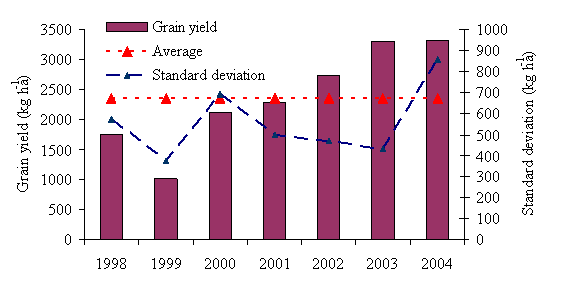
Figure 1.Winter wheat grain yield, overall mean and standard deviation across years at Perkins, OK
Table 1. Initial surface (0-15cm) Soil chemical characteristics at Perkins, OK, 1996.
|
pH |
NH4-N |
NO3-N |
P |
K |
Total N |
Organic Carbon |
|
|
--------------------------mg kg-1----------------------------- |
------------g kg-1------------ |
||||||
|
5.95 |
3.04 |
2.83 |
8.99 |
133.0 |
0.504 |
5.34 |
|
pH: 1:1 soil:water Organic C and Total N: dry combustion, NH4-N and NO3-N: Lachat P and K: Mehlich-3
Table 2. Mean wheat grain yield and probabilities of polynomial orthogonal contrasts at Perkins, OK, 1998-2004.
|
Source |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
|
N, kg ha-1 |
---------------------------Yield, kg ha-1------------------------------ |
||||||
|
0 |
1147 |
584 |
1654 |
2306 |
2769 |
2744 |
2087 |
|
56 |
1602 |
954 |
2418 |
2472 |
2804 |
3510 |
3599 |
|
112 |
2063 |
1233 |
2297 |
2316 |
2683 |
3493 |
3877 |
|
168 |
2196 |
1269 |
2161 |
2026 |
2686 |
3488 |
3697 |
|
Linear |
*** |
*** |
P<0.1 |
NS |
NS |
*** |
*** |
|
Quadratic |
NS |
NS |
* |
NS |
NS |
*** |
*** |
|
|
|
|
|
|
|
|
|
|
P, kg ha-1 |
---------------------------Yield, kg ha-1------------------------------ |
||||||
|
0 |
1535 |
823 |
2514 |
2317 |
2680 |
3242 |
3492 |
|
15 |
1744 |
1045 |
2279 |
2398 |
2680 |
3322 |
3457 |
|
30 |
1978 |
1163 |
1593 |
2130 |
2847 |
3362 |
2996 |
|
Linear |
*** |
*** |
*** |
NS |
NS |
NS |
*** |
|
Quadratic |
NS |
NS |
NS |
NS |
NS |
NS |
NS |
*, **, *** Significant at the 0.10, 0.05, and 0.01 levels of probability, respectively; NS is not significant.
Table 3. Mean nitrogen content (g kg-1) and probabilities of polynomial orthogonal contrasts at Perkins, OK, 1998-2004.
|
Source |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
|
N, kg ha-1 |
--------------------- nitrogen content, g kg-1 ----------------------- |
||||||
|
0 |
20.6 |
21.5 |
19.1 |
37.7 |
20.3 |
19.2 |
17.6 |
|
56 |
21.2 |
21.7 |
21.1 |
23.6 |
25.0 |
22.5 |
21.0 |
|
112 |
23.1 |
24.2 |
22.1 |
25.2 |
27.2 |
24.9 |
24.8 |
|
168 |
23.5 |
27.7 |
25.9 |
26.0 |
27.7 |
27.2 |
29.1 |
|
Linear |
*** |
*** |
*** |
NS |
*** |
*** |
*** |
|
Quadratic |
NS |
NS |
NS |
NS |
NS |
NS |
NS |
|
P, kg ha-1 |
--------------------- nitrogen content, g kg-1 ----------------------- |
||||||
|
0 |
22.7 |
25.3 |
22.3 |
24.1 |
24.8 |
23.0 |
23.0 |
|
15 |
21.9 |
22.8 |
21.3 |
37.1 |
25.4 |
23.3 |
22.8 |
|
30 |
21.8 |
23.2 |
22.6 |
25.2 |
25.0 |
24.1 |
23.6 |
|
Linear |
NS |
* |
NS |
NS |
NS |
NS |
NS |
|
Quadratic |
NS |
* |
NS |
* |
NS |
NS |
NS |
*, *** Significant at the 0.05 and 0.001 levels of probability, respectively; NS is not significant.
Table 4. Parameter estimates, probabilities, and partial squared correlation coefficients for effect of N and year indicator variables on grain yield of winter wheat at Perkins, OK.
|
Parameter |
Variable |
Estimate |
Pr > |t| |
SPCORR1† |
SPCORR2‡ |
|
b0 |
|
1910 |
*** |
. |
. |
|
b1 |
N |
3.52 |
*** |
0.05 |
0.150 |
|
b2 |
1998 |
-453 |
*** |
0.07 |
0.06 |
|
b3 |
1999 |
-1195 |
** |
0.46 |
0.33 |
|
b5 |
2002 |
531 |
*** |
0.00 |
0.08 |
|
b6 |
2003 |
1104 |
*** |
0.12 |
0.29 |
|
b7 |
2004 |
1110 |
*** |
0.29 |
0.29 |
**, and *** Significant at the 0.01, and 0.001 levels of probability, respectively
† the squared partial correlation coefficients calculated using Type I sequential sum square
‡ the squared partial correlation coefficients calculated using Type III partial sum square