J.M. LaRuffa, W.R. Raun, S.B. Phillips, J.B. Solie, M.L. Stone, and G.V. Johnson

ABSTRACT

The resolution at which variability in soil test and yield parameters exists is fundamental to the efficient use of real-time sensor-based variable rate technology.  This study was conducted to determine the optimum field element size for maximum yields in winter wheat (Triticum aestivum L.) using variable nitrogen rates based on sensor readings.  The effect of applying N at four different resolutions (0.84, 3.34, 13.38 and 53.51m²) on grain yield, N uptake and efficiency of use was investigated at Haskell, Hennessey, Perkins, and Tipton, Oklahoma.  At Feekes growth stage 5 an optical sensor developed at Oklahoma State University measured red (670± 6 nm) and near-infrared (NIR, 780±6 nm) reflectance in each subplot.  A normalized-difference-vegetative-index (NDVI) was calculated from the sensor measurements.  Nitrogen was applied based on a NDVI – N rate calibration.  Nitrogen rate, yield, N uptake, and efficiency of use responses to treatment resolution and applied N fertilizer differed in the three years of this experiment.  In the first year, no significant influence of resolution on N rate, yield, N uptake, or efficiency of use was observed, likely a result of a late freeze that drastically reduced yields.  In the second year of the experiment, there was a trend for a lower N rate and a higher efficiency of use for the 0.84 m² resolution.  In the third year of this study, there was a trend for a higher yield and a higher efficiency of use for the 53.51 m² resolution at both sites.  In general, the finer resolutions tended to have increased efficiency of use in high yielding environments (>2300 kg ha^-1), and decreased yields in low yielding environments.  This study indicates that application of prescribed fertilizer rates based on spatial variability at resolutions finer than 53.51m² could lead to increased yields, decreased grower costs, and decreased environmental impact of excess fertilizers.

INTRODUCTION

Soil testing is the most widely used method to detect nutrient availability.  However, a composite sample estimates the mean soil test nutrient level which does not address the variability encountered in that field (Raun et al., 1998).  Optical sensor-based variable rate technology (s-VRT) has the ability to detect submeter-variability of nutrients on-the-go and simultaneously apply prescribed fertilizer rates based on those needs, thus realizing the potential to increase yields, decrease grower costs, and decrease the environmental impact of excess fertilizers.  In order to effectively utilize s-VRT, Sawyer (1994) suggested that within-field variation must be accurately identified and reliably interpreted.  Therefore, there is a need to establish the optimum field element size, which is fundamental to s-VRT in order to detect micro-variability of nutrients, such as nitrogen.  Solie et al. (1996) defined the optimum field element size as that area which provides the most precise measure of the available nutrient where the level of that nutrient changes with distance.  They proposed 0.8 to 1.4 m as the range for the field element size.  The field element size should identify the smallest resolution where cause and effect relationships can be measured, where misapplication could pose a risk to the environment, where net economic return can be achieved, and where differences in yield potential may exist (Raun et al., 1998).  Sensing need and applying fertilizer based on the optimum field element size should provide the most precise measurement of actual crop need and its application to the crop (Solie et al., 1996).

            Sawyer (1994) recently pointed out that on-the-go sensing was still futuristic; however, new developments by Stone et al. (1996) have demonstrated that optical sensor based variable rate application systems are capable of detecting nutrient variability, and research is being conducted to more fully develop s-VRT.  The initial optical sensor based system at Oklahoma State University measured spectral irradiance or light energy per unit area of the target crop.  Irradiance is sensitive to sunlight, illumination angle, crop direction, and cloud cover.  The current sensor based system measures reflectance.  Spectral irradiance measurements are obtained using an integrated sensor with photodiode-based sensors and interference filters for red (671± 6 nm) and near infrared (NIR, 780 ± 6 nm) (Stone et al., 1996b).  Up-oriented and down-oriented sensors measure solar spectral irradiance (incident radiation) and plant surface irradiance (reflected radiation), respectively.  Reflectance values are calculated as a ratio of the incident and reflected radiation.  Measurements taken at these wavelengths can be used to calculate a normalized-difference-vegetative-index (NDVI), which has been demonstrated to be highly correlated with plant N uptake (Stone et al., 1996a), and a reliable predictor of topdress N needs (Roth et al., 1989).  The objective of this study was to determine the optimum field element size for maximum yields in winter wheat using variable nitrogen rates based on sensor readings and the calculated NDVI values.

MATERIALS AND METHODS

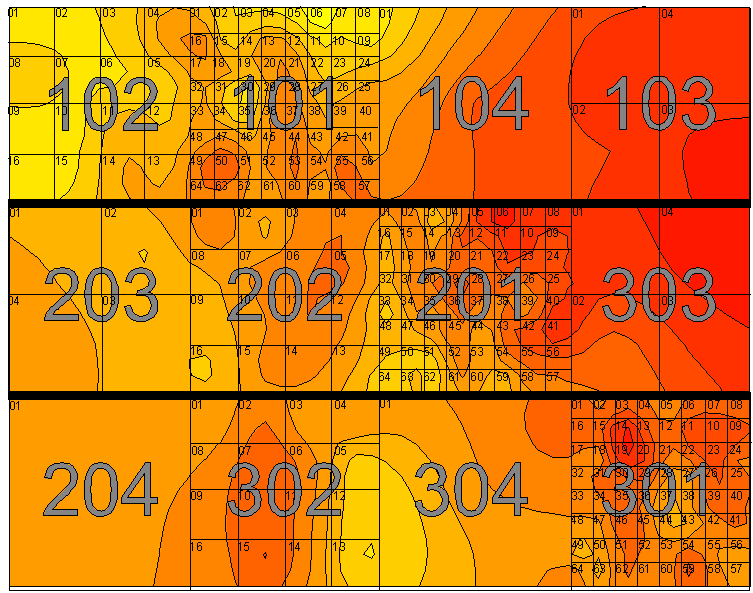
Two studies were initiated in January 1997 at Tipton and Hennessey, Oklahoma.  The study was continued in 1998 at Tipton and Perkins, Oklahoma and in 1999 at Tipton and Haskell, Oklahoma.  Soil types and initial soil test results are reported in Table 1.  Most sites  were N deficient, but had no P or K deficiencies.  Winter wheat (Triticum aestivum L.) ‘Tonkawa’ had been previously established at all sites at 78 kg ha^-1 seeding rate.  Wheat was planted in early October using 0.19 m row spacing.  No preplant N was applied to any site in any year.  At each location, a completely randomized design was employed.  Four levels of resolution (field element size) were evaluated in a randomized complete block design with three replications.  Resolutions tested were 0.91 by 0.91m, 1.83 by 1.83 m, 3.66 by 3.66m and 7.32 by 7.32m or 0.83, 3.34, 13.38, 53.31 m², respectively.  Plot size for all treatments was 7.32 by 7.32m with main plots subdivided by the appropriate number of subplots for each resolution (Figure 1).  In addition, planting , sensing, fertilization, and harvest dates at each site are reported in Table 2.

At Feekes growth stage 5 (Large, 1954) an optical sensor developed at Oklahoma State University measured red (671± 6 nm) and near-infrared (NIR, 780±6 nm) wavelengths in each subplot.  The sensor was mounted on the front of a John Deere model 318 lawn and garden tractor with a field-of-view of 0.91 m x 0.15 m.  Approximately 10 readings were taken per 0.84 m² area.  In 1996-97, a normalized-difference-vegetative-index (NDVI) was calculated from the sensor measurements obtained for red and NIR uncalibrated voltage readings, according to the following equation, NDVI = (NIR-red)/(NIR+red).

In 1997-98, NDVI was calculated from calibrated voltage readings that accounted for incoming light.  The sensor used in these tests measured both incident and reflected radiation.  Field-of-view was the same as that in the 1996-97 experiments.  Reflectance values (the ratio of incident and reflected values) were used in the NDVI calculation to minimize the error associated with cloud cover, shadows and sun angle.  The modified equation used in 1997-98 was; NDVI = [(NIR_ref/NIR_inc)-(Red_ref/Red_inc)]/[(NIR_ref/NIR_inc)+(Red_ref/Red_inc)]  where NIR_ref and Red_ref = magnitude of reflected light, and NIR_inc and Red_inc = magnitude of the incident light.

In 1996-97, variable N rates were determined for the subplots based on a linear NDVI - N rate scale.  Subplots with the lowest NDVI values received the highest fertilizer N rate (112 kg ha^-1) and the highest NDVI values received the lowest fertilizer N rate (0 kg ha^-1).  Linear regression models were calculated in Excel (Table 3).  An identical linear NDVI – N rate scale was utilized at Perkins in 1997-98.  However, a ramped NDVI – N rate scale was utilized at Tipton in 1997-98 to account for variation in percent coverage or stand density.  The linear NDVI - N rate scale was based on previous work reported by Stone et al. (1996a). 

In 1998-99, nitrogen fertilization rates were based on the in-season estimated yield or INSEY index (Raun et al., 1999).  Based on previous work, INSEY was computed using the sum of NDVI at Feekes 4 and NDVI at Feekes 5, divided by the growing degree days from Feekes 4 to Feekes 5.  Nitrogen fertilizer rates were then determined using the following equation:

N rate =[(Predicted grain yield *%N in the grain)–(Predicted forage N uptake at Feekes 5)]/0.70

where predicted grain yield was estimated from INSEY, %N in the grain was obtained from average values associated with winter wheat at different yield levels, and predicted forage N uptake at Feekes 5 was based on the relationship with NDVI (Raun et al., 2000). 

Each year the amount of N fertilizer for each subplot was determined and the appropriate amount of ammonium nitrate was broadcast applied by hand.  Each location was harvested with a Massey Ferguson 8XP self-propelled combine in June and early July (Table 2).  The entire subplot area was harvested and grain weights and percent moisture were automatically recorded.  Pre-harvest calibration of the combine scales indicated that weights had precision of ± 15.44 g.  Grain samples were collected and weighed on lab scales when yields were low (<50 g).  Grain was ground to pass a 106 um (140 mesh) screen and total nitrogen content in grain was analyzed using a Carlo Erba NA 1500 dry combustion analyzer (Schepers et al., 1989).  The efficiency of use index was calculated as grain yield/N rate (Moll et al., 1982).  Nitrogen uptake was determined by multiplying percent N in the grain by grain yield.  Statistical analysis was performed using SAS (SAS Institute, 1988).

RESULTS

Response to treatment resolution and applied N fertilizer differed over the three years and four locations.  Results from each location and year are discussed separately due to the contrasting response. 

Hennessey, 1996-97

            There was no significant influence of resolution on N rate, yield, N uptake, or efficiency of use (Table 4).  The NDVI values for this location ranged from 0.70 to 0.81 (mean of 0.78 ± 0.01) and were normally distributed.  In general, NDVI values in excess of 0.70 indicate that plant coverage of the soil was equal to or greater than 70% (Lukina et al., 1999).  At the early stages of growth evaluated here, this also indicated that plant health was excellent for the entire experimental area and that plot to plot variability was likely small.  Also, the CV (coefficient of variation) for NDVI was very low (1%), indicating that limited variability existed at this site.  A large portion of the experiment had high NDVI values (high N uptake) and was likely non-responsive.  Because of this, low N rates were applied to areas where no response was expected and high N rates were applied where only limited increases were realistic. 

Tipton, 1996-97

            NDVI values at this location ranged from 0.18 to 0.48 (mean of 0.34 ± 0.05) and were normally distributed.  More variability in NDVI was found at this site than the Hennessey site.  Grain yields were drastically lower at Tipton compared to Hennessey due to freeze damage on April 11, 12 and 13.  There was no significant influence of resolution on N rate, yield, N uptake or efficiency of use (Table 5).  However, it should be noted that the poor stands (evidenced in the low NDVI’s) were the result of moisture limiting conditions that lowered yield potential.  Therefore, the chances of observing a response to added fertilizer at any of the treatment resolutions were poor.  

Perkins, 1997-98

            NDVI values at this location ranged from 0.28 to 0.63 (mean of 0.42 ± 0.05) and were normally distributed.  The linear NDVI – N rate scale used was expected to encompass the entire range of N needs (maximum N need at NDVI = 0.28 and limited N need at NDVI = 0.63).  There was no significant influence of resolution on N rate, yield, N uptake or efficiency of use (Table 6).  However, there was a trend for a lower N rate and a higher efficiency of use for the 0.84 m² resolution.  Although nitrogen uptake was somewhat lower for the finest resolution (0.84 m²), it was important to find that the standard deviation was lower at this resolution when compared to coarser resolutions (means of 51.53 ± 1.88, 52.30 ± 5.81, 54.21 ± 4.67, and 60.27 ± 6.63 for the 0.84, 3.34, 13.38, 53.51 m² resolutions, respectively).  This suggests that topdress N fertilization based on predicted forage N uptake (every 0.84 m²) at early stages of growth could result in homogeneity of grain yield.  Furthermore, it was important to note that the CVs separated by treatment for yield and efficiency of use were lowest for the 0.84 m² resolution (Table 7), suggesting that small-scale management assisted in decreasing treatment heterogeneity.

Tipton, 1997-98

            NDVI values at this location ranged from 0.28 to 0.79 (mean of 0.56 ± 0.08) with a bimodal distribution.  Grain yields increased for the coarser resolutions at this site (Table 8).  There was no significant influence of resolution on N rate, efficiency of use or N uptake.  However, there was a trend for a higher efficiency of use at the 0.84 m² resolution, supported in part by a significant quadratic relationship between efficiency of use and resolution.  The CVs separated by treatment for yield and efficiency of use were lowest for the 13.38 m² resolution (Table 9).  This suggests that micro-variability was better managed at a resolution less than 53.51 m² but not necessarily at the 0.84 m² resolution that we expected.  This supports management of resolutions of 13.38m², much finer than anything presently promoted in commercial agriculture.

Haskell, 1998-99

            INSEY values at this location ranged from 0.0043 to 0.0069 (mean of 0.0057 + 0.0005).  There was no significant influence of resolution on N rate, grain yield, N uptake, or efficiency of use (Table 10).  However, there was a trend for a higher N rate, yield, N uptake, and efficiency of use at the 53.51 m² resolution.  A significant linear relationship was found between yield and resolution and N uptake and resolution.  However, it should be noted that this observation took place at low yield levels (<1750 kg ha^-1).

Tipton, 1998-99

            INSEY values at this location ranged from 0.0027 to 0.0059 (mean of 0.0038 + 0.0005).  Similar to results at Haskell, 1998-99, a trend for increased N uptake and grain yield at the coarser resolutions was observed, but at low yield levels. 

Discussion

            The lack of differences due to management resolution noted in this study may have been due to several factors that were not initially considered.  Using the John Deere 318 lawn and garden tractor to sense each 0.84m² area in all 24 subplots for the 0.84m² resolution increased soil compaction, reduced forage growth, and decreased yields when compared to the coarser resolutions that required few passes over main plots.  The range of INSEY values for the 1998-99 cropping season was unusually narrow when observing other data reported for wheat (Raun et al., 2000).  This in turn limited the likelihood of observing yield differences as a result of treating within plot variability.  The strategies used to adjust fertilizer N based on sensor readings differed for all three years of the study.  Changes in the N fertilization strategy were made based on increased understanding of problems encountered in other ongoing projects.  Lastly, the lack of notable statistical treatment differences could have been due to the low grain yields found at all sites in all years.  Nitrogen availability although normally limiting, likely was only a minor factor affecting grain yield under these conditions.  Some of the main factors limiting grain yields for the locations and years evaluated included poor stands, late harvest, lodging, and compaction.

CONCLUSIONS

The effect of applying N at four different resolutions (0.84, 3.34, 13.38 and 53.51m²) on wheat grain yield, N uptake and efficiency of use was investigated from 1996 to 1999.  Sensor readings were collected at Feekes growth stage 5 and subsequently used to determine topdress N rates based on predicted forage N uptake.  In general, the finer resolutions tended to have increased efficiency of use in high yielding environments (>2300 kg ha^-1), and decreased efficiency of use in low yielding environments.  Although not consistent over the years included in this work, application of prescribed fertilizer rates based on spatial variability at resolutions finer than 53.51m² could lead to increased yields, decreased grower costs, and decreased environmental impact of excess fertilizers.

REFERENCES

Large, E.C.  1954.  Growth stages in cereals.  Plant Pathol. 3:128-129.

Lukina, E.V., M.L. Stone and W.R. Raun. 1999. Estimating vegetation coverage in wheat using digital images. J. Plant Nutr. 22(2):341-350.

Moll, R.H., E.J., Kamprath, and W.A. Jackson.  1982.  Analysis and interpretation of factors which contribute to efficiency of nitrogen utilization.  Agron J. 74:562-564.

Raun, W.R., J.B. Solie, G.V. Johnson, M.L. Stone, R.W. Whitney, H.L. Lees, H. Sembiring, and S.B. Phillips.  1998.  Micro-variability in soil test, plant nutrient and yield parameters.  Soil Sci. Soc. Am. J. 62:683-690. 

Raun, W.R., G.V. Johnson, M.L. Stone, J.B. Solie, W.E. Thomason and E.V. Lukina. 1999. In-season prediction of yield potential in winter wheat. Better Crops 83(2): 24-25.

Raun, W.R., J.B. Solie, M.L. Stone, G.V. Johnson, E.V. Lukina, W.E. Thomason and J.S. Schepers. 2000. In-season prediction of wheat yield potential using canopy reflectance. (Agron. J.)

Roth, G.W., R.H. Fox, and H.G. Marshall.  1989.  Plant tissue tests for predicting nitrogen fertilizer requirements of winter wheat.  Agron. J. 81:502-507.

SAS Institute Inc.  1988.  SAS/STAT User’s Guide.  6.03 ed.  SAS Institute Inc., Cary, NC.

Sawyer, J.E.  1994.  Concepts of variable rate technology with considerations for fertilizer application.  J. Prod. Agric. 7:195-201.

Schepers, J.S., D.D. Francis, and M.T. Thompson.  1989.  Simultaneous determination of total C, total N, and 15N on soil and plant material. Commun. in Soil Sci. Plant Anal.  20(9&10):949-959.

Solie, J.B., W.R. Raun, R.W. Whitney, M.L. Stone, J.D. Ringer.  1996. Optical sensor based field element size and sensing strategy for nitrogen application. Trans. ASAE 39(6):1983-1992.

Stone, M.L., J.B. Solie, R.W. Whitney, W.R. Raun, and H.L. Lees.  1996a. Sensors for detection of nitrogen in winter wheat.  SAE Technical paper series.  SAE Paper No. 961757.   SAE, Warrendale PA.

Stone, M.L., J.B. Solie, W.R. Raun, R.W. Whitney, S.L. Taylor, and J.D. Ringer. 1996b.  Use of spectral radiance for correcting in-season fertilizer nitrogen deficiencies in winter wheat.  Trans. ASAE 39(5):1623-1631.

TABLE 1.  Initial surface (0-15 cm) soil test characteristics prior to treatment application, and soil classification at Haskell, Hennessey, Perkins, and Tipton, Oklahoma.

TABLE 2.  Planting , sensing, fertilization, and harvest dates, 1996-1999.

_____________________________________________________________________

Location            Planting Date     Sensing Date      Fertilization Date         Harvest Date

Hennessey        10/02/96            02/11/97             02/13/97                     07/25/97

Tipton               10/07/97            02/04/97             02/06/97                     07/12/97

Perkins             10/21/97            02/24/98             03/04/98                     06/16/98

Tipton               10/16/97            01/27/98             02/12/98                     06/07/98

Haskell             10/26/98            02/24/99             03/23/99                     07/06/99

Tipton               10/08/98            02/09/99             03/02/99                     06/07/99
_____________________________________________________________________

TABLE 3.  Linear regression models developed for a linear NDVI – N rate scale.

* x = NDVI; y = N rate

TABLE 4.  Analysis of variance for NDVI, nitrogen rate, grain yield, nitrogen uptake, and efficiency of use in wheat at Hennessey, OK, 1996-97.

* Significant at the 0.05 probability level; df = degrees of freedom; ns = not significant; SED = standard error of the difference between two equally replicated treatment means; CV = coefficient of variation

TABLE 5.  Analysis of variance for NDVI, nitrogen rate, grain yield, nitrogen uptake, and efficiency of use in wheat at Tipton, OK, 1996-97.

* Significant at the 0.05 probability level; df = degrees of freedom; ns = not significant; SED = standard error of the difference between two equally replicated treatment means; CV = coefficient of variation.

TABLE 6.  Analysis of variance for NDVI, nitrogen rate, grain yield, nitrogen uptake, and efficiency of use in wheat at Perkins, OK, 1997-98.

* Significant at the 0.05 probability level; df = degrees of freedom; ns = not significant; SED = standard error of the difference between two equally replicated treatment means; CV = coefficient of variation

TABLE 7.  Coefficients of variation, by treatment, for grain yield and efficiency of use in wheat at Perkins, OK, 1997-98.

TABLE 8.  Analysis of variance for NDVI, nitrogen rate, grain yield, nitrogen uptake, and efficiency of use in wheat at Tipton, OK, 1997-98.

* Significant at the 0.05 probability level; df = degrees of freedom; ns = not significant; SED = standard error of the difference between two equally replicated treatment means; CV = coefficient of variation.

TABLE 9.  Coefficients of variation, by treatment, for grain yield and efficiency of use in wheat at Tipton, OK, 1997-98.

TABLE 10.  Analysis of variance for INSEY, nitrogen rate, grain yield, nitrogen uptake, and efficiency of use in wheat at Haskell, OK, 1998-99.

* Significant at the 0.05 probability level; df = degrees of freedom; ns = not significant; SED = standard error of the difference between two equally replicated treatment means; CV = coefficient of variation

TABLE 11.  Analysis of variance for INSEY, nitrogen rate, grain yield, nitrogen uptake, and efficiency of use in wheat at Tipton, OK, 1998-99.

* Significant at the 0.05 probability level; df = degrees of freedom; ns = not significant; SED = standard error of the difference between two equally replicated treatment means; CV = coefficient of variation

FIGURE 1.  Diagram of the physical layout of the experiments showing treatments (1-4) and resolution within treatment.