¹Department of Plant and Soil Sciences, ²Department of Biosystems and Agricultural Engineering, Oklahoma State University, Stillwater, Ok 74078. Contribution from the Oklahoma Agricultural Experiment Station. *Corresponding author.

ABSTRACT

Current methods of determining nitrogen (N) fertilization rates in winter wheat (Triticum aestivum L.) are based on farmer projected yield goals and fixed N removal rates per unit of grain produced. This work reports on an alternative method of determining fertilizer N rates using estimates of early-season plant N uptake and potential yield determined from in-season spectral measurements collected between January and April. Reflectance measurements under daytime lighting in the red and near infrared regions of the spectra were used to compute the normalized difference vegetation index (NDVI). Using a modified daytime lighting reflectance sensor, early-season plant N uptake between Feekes physiological growth stages 4 (leaf sheaths lengthen) through 6 (first node of stem visible) was found to be highly correlated with NDVI. Further analyses showed that dividing the NDVI sensor measurements between Feekes growth stages 4 and 6, by the days from planting to sensing date was highly correlated with final grain yield. This in-season estimate of yield (INSEY) was subsequently used to compute the potential N that could be removed in the grain. In-season N fertilization needs were then considered to be equal to the amount of predicted grain N uptake (potential yield times grain N) minus predicted early-season plant N uptake (at the time of sensing), divided by an efficiency factor of 0.70. This method of determining in-season fertilizer need has been shown to decrease large area N rates while also increasing wheat grain yields when each 1m2 area was sensed and treated independently.

INTRODUCTION
    The word precision, is defined as 'the quality or state of being precise, or exactness.' In many ways, precision agriculture is still being defined, but it certainly must include 'being precise, or exact' in the management of agronomic and engineering variables. The development of a precision agriculture technology (PAT) would imply that it resulted in a more precise measurement and treatment of the independent variables than had been achieved before. In this regard, the scientific community has the responsibility of making sure that each new PAT result in a measurable improvement (application, management, monitoring, and/or mapping). The measurable improvement could be decreased inputs with no sacrifice in yield, or increased yield at the same level of inputs (improved efficiency) for the specific variable being evaluated. One of the more radical hypotheses was recently posed by Solie et al. (1999) who contended that the area over which variable rate fertilizer applicators should sense and apply materials is likely to be 1.0 by 1.0 m or smaller. Taking this a step further suggests that each PAT applied to field crop production must be evaluated at a resolution less than or equal to 1.0m2. This challenge has been recognized since various research programs have already noted that spatially variable N fertilizer application may reduce adverse environmental impacts and increase economic return (Fiez et al., 1995)
    Filella et al. (1995) noted that remote sensing could provide inexpensive, large-area estimates of N status and be used to monitor N status, since leaf chlorophyll A content is mainly determined by N availability. They further reported that the use of reflectance at 430 nm, 550 nm, 680 nm, and red edge wavelengths offers potential for assessing N status of wheat. Work with winter wheat by Raun et al. (2000) found that two post-dormancy NDVI measurements (reflectance of red and near infrared in January and March) divided by the cumulative growing degree days from the first to the second reading could be used to predict potential grain yield. They also indicated that if potential grain yield could be predicted in-season, topdress N rates could be based on predicted yield.
    Sowers et al. (1994) reported that reduced N rates and split N applications between fall and spring can maintain high yields but at reduced grain protein levels. It is therefore conceivable, that if variable rate technology resulted in applied N based on projected need or potential yield (some areas receive added N, some do not), average grain protein levels may not decrease in fields where N was applied using variable rate technology.
    An area where PAT's will likely be beneficial is in the identification of sustainable production practices and management tools. Halvorson et al. (1999) recently reported that increases in soil organic carbon, improved soil quality and productivity with increased N fertilization. Capitalizing on the spatial variability known to exist in agricultural fields reported by Solie et al. (1999), precision applied N could increase C sequestration (on average) when compared to flat rates.
    On a global scale, Tilman (1999) reported that the doubling of agricultural food production during the past 34 years was associated with a 6.87-fold increase in N fertilization, 3.48-fold increase in P fertilization, 1.68-fold increase in the amount of irrigated cropland and a 1.1-fold increase in land in cultivation. This work further noted that the next doubling of global food production would be associated with a 3-fold increase in N and P fertilization rates, doubling of the irrigated land area, and an 18% increase in cropland. Therefore, it seems plausible that PAT's could fill a large forecasted void regarding world food production and the need for sustainable agricultural systems.
    The objectives of this work were (i) to determine the feasibility of using a single optical sensor measurements to predict early-season plant N uptake for readings obtained over locations, stages and years, (ii) to determine the best method to empirically calibrate optical sensor measurements with potential wheat grain yield when readings are made at different growth stages, geographical locations and in different years, and (iii) propose a procedure to use optically sensed estimates of early season plant N uptake and potential yield to calculate N fertilizer application rate.

MATERIALS AND METHODS
    During the winter months of 1998, 1999 and 2000, spectral reflectance readings were taken from 9 winter wheat experiments to refine estimates of early-season plant N uptake at or near Feekes growth stage 5 and from 16 experiments to refine estimates of potential grain yield. Each experiment was either an on-going long-term experiment (numbers assigned in the 1960's and 1970's as 222, 301, 502 and 801), a short-term (1-3 years) field experiment that included the evaluation of preplant N rates, or transects (50, 1x1m continuous plots). The early-season plant N uptake and potential yield experiments are further defined in Tables 1 and 2, respectively. The soils at each of these locations are; Perkins, Teller sandy loam (fine-loamy, mixed, thermic Udic Argiustolls); Tipton, Tipton silt loam (fine-loamy, mixed, thermic Pachic Argiustolls); Stillwater, Kirkland silt loam (fine, mixed, thermic Udertic Paleustolls); Efaw, Norge silt loam (fine-silty, mixed, thermic Udic Paleustolls); Lahoma, Grant silt loam (fine-silty, mixed, thermic Udic Argiustolls); and Haskell, Taloka silt loam (fine, mixed, thermic Mollic Albaqualfs). The row spacing by N rate (S*N), Efaw anhydrous ammonia (AA), and transect experiments were each one-year trials. The N rate by P rate (N*P) experiment at Perkins was initiated in 1996. Experiments 222, 301 and 502 were initiated in 1969, 1993 and 1971, respectively, and all three evaluated annual rates of applied N at constant levels of P and K (Table 1). Winter wheat was planted at a 78 kg ha-1 seeding rate using a 0.19 m row spacing, excluding the S*N experiment at Perkins (spacing ranged from 0.15 to 0.30 m). Varieties used in each trial are reported in Tables 1 and 2.
    Spectral reflectance was measured using an Oklahoma State University designed instrument that included two upward directed photodiode sensors, and that received incident light through cosine corrected Teflon® windows fitted with red (671±6nm) and near-infrared (NIR)(780±6nm) interference filters. The instrument also included two down-looking photodiode sensors that received light through collination and interference filters identical to the up-looking sensors. The instrument used a 16 bit A/D converter to simultaneously capture and convert the signals from the four photodiode sensors. Collination was used to constrain the view of the down-looking sensors to a 0.84 m2 oblong area at the plant surface. Stability of the sensor was maintained across time by calibration with a barium sulfate coated aluminum plate. The reflectance of the barium sulfate coated plate was assumed to be 1.0 for both spectral bands investigated. Reflectance values (the ratio of incident and reflected values) were used in the NDVI calculation to minimize the error associated with cloud cover, shadows and sun angle. Reflectance based NDVI was calculated using the following equation: NDVI = [(NIRref/NIRinc)-(Redref/Redinc)] / [(NIRref/NIRinc)+(Redref/Redinc)], where NIRref and Redref = magnitude of reflected light, and NIRinc and Redinc = magnitude of the incident light.
    Although 4 different wheat varieties are included in this work, varietal differences were not targeted, since findings of Sembiring et al. (2000) showed limited differences in post-dormancy NDVI readings for common wheat varieties grown in this region. Reflectance readings from all experiments were collected at two post-dormancy dates. The two dates (Time-1 and Time-2, respectively) where readings were collected ranged between Feekes growth stage 4 (leaf sheaths beginning to lengthen), 5 (pseudo-stem, formed by sheaths of leaves strongly erect), and 6 (first node of stem visible)(Large, 1954). For the early-season plant N uptake and grain yield potential experiments, individual wheat plot reflectance readings were taken from 1.0 m2 and 4.0m2 areas, respectively, between 10 a.m. and 4 p.m under natural lighting. For the early-season plant N uptake experiments (Table 1), individual 1m2 plots were hand clipped (immediately following sensor readings) and weighed prior to being dried in a forced air oven at 60°C. Once dry, samples were ground to pass a 0.125mm (120-mesh) sieve and analyzed for total N using a Carlo Erba (Milan, Italy) NA-1500 dry combustion analyzer (Schepers et al., 1989). Early-season plant N uptake was determined by multiplying dry matter yield by the total N concentration determined from dry combustion.
    In the grain potential yield trials, grain yield was determined using a self propelled combine from the same 4.0 m2 area where spectral reflectance data were collected. We assumed that growth from planting in October to the mid winter months of January and February would provide an excellent indicator of wheat health in each 4.0 m2 area and the influence of early-season growth-limiting conditions for small areas. In-season estimated yield, or INSEY, was determined by dividing NDVI sensor measurements between Feekes growth stages 4 and 6 by the days from planting to the date sensor measurements were taken. A number of possible indices relating NDVI to wheat yield were investigated. Indices were ranked by regression (R2) and the index with the highest R2 for all dates was selected for estimating potential grain yield. Because NDVI at Feekes 4-6 has been shown to be an excellent predictor of early-season plant N uptake, the INSEY value reported here represents plant N uptake per day. The use of days from planting to sensing in the computation of INSEY allowed us to predict the early-season plant N uptake per day from sites where planting to sensing ranged from 123 to 167 days (Table 2).
    Following initial indices of estimated yield (EY) reported by Raun et al. (2000), the INSEY index reported here was one of many indices evaluated that included mathematical combinations of NDVI at various growth stages, days from planting to sensing times, growing degree days (GDD) from planting to sensing, and days, and GDD between sensor readings (GDD = [(Tmin + Tmax)/2 - 4.4°C] (Tmin and Tmax recorded from daily data).
    Measured grain yield was considered to be the best available measure of potential grain yield, especially where limited stress occurred after sensor readings in late February and early March. Linear, quadratic, logarithmic and exponential models were evaluated that included all locations and data subsets using various indices to predict grain yield.

RESULTS
    The relationship between early-season plant N uptake and NDVI for the nine experiments where forage biomass, forage N and sensor readings were collected between Feekes growth stages 4 and 6, is reported in Figure 1. NDVI was an excellent predictor of early-season plant N uptake for these nine trials that covered three years, two varieties, a range of planting and sensing dates, and three physiological stages of growth. Earlier work by Sembiring et al. (2000) reported high correlation between early-season plant N uptake and NDVI between Feekes growth stages 4 and 8. However, they reported that specific by-stage early-season plant N uptake calibration would be needed when using NDVI as a predictor, since the linear regression equations differed significantly by stage. To some extent this was expected since the NDVI readings used in their work (earlier version of the sensor employed in this work) were not calibrated to account for changing light (sun angle, clouds, shadows) when recording sensor readings from one time (day, month, location) to the next. Using the reflectance based NDVI equation and the improved sensor which measured both incident and reflected radiance, early-season plant N uptake could now be reliably predicted (R2=0.75) over stage of growth (Figure 1). It is important to note that an average of 45 kg N ha-1 was taken up in the forage for all nine experiments (Figure 1) and that this represents over half of the total N that would end up in the grain (average yield of 2.52 Mg ha-1 would have 63 kg N ha-1 removed in the grain when grain N % = 2.5, Thomason et al., 2000). Therefore, a large portion of the potential-yield-N is assimilated by early to mid-February, which is four months before harvest.
    In addition to being a reliable predictor of early-season plant N uptake between Feekes growth stages 4 and 6, NDVI readings taken at these same stages were positively correlated with final grain yield (Figure 2). Although these results were encouraging, data from several locations over this three-year period clearly did not fit the general trend (Figure 2). Earlier work by Raun et al. (2000) noted that the sum of NDVI readings at Feekes 4 and Feekes 5, divided by the cumulative GDD between readings was a reliable predictor of wheat grain yield at 6 of 9 locations. Their work was considered to be somewhat cumbersome since it relied on two post-dormancy sensor readings to predict wheat grain yield. Further analyses of these same 9 trials, plus 7 more locations (total of 16) showed that NDVI divided by the total number of days from planting to sensing was better correlated (R2 of 0.64 compared to R2 of 0.53) with wheat grain yield. More importantly, this in-season estimate of yield (INSEY) included all sixteen sites over a three-year period, and that was clearly an improvement upon the EY equation initially reported by Raun et al. (2000).
    Dividing NDVI at Feekes 5 (excellent predictor of early-season plant N uptake, Figure 1) by the days from planting to the NDVI sensing date resulted in an index that would approximate N uptake per day. This estimate of N uptake per day could be viewed as the rate at which N was accumulated from October to March. Equally important for this compiled data was knowing that the days from planting to sensing (INSEY divisor) ranged from 123 to 167 days. Even if the range in inclement mid-winter weather varied by 10 to 30 days (from one site to the next), the total number of days for potential growth would be a plausible divisor for the in-season NDVI measurement. It should be noted that almost all of the measurements were made after winter wheat had broken dormancy, thus exhibiting more rapid growth. Considering that three years of data, sixteen site-years, and differing planting and sensing dates were included in this work, the new INSEY index clearly provided a common linkage for a holistic model (Figure 3). This was also evident when plotting wheat grain yield as a function of INSEY for each of the years where data was recorded, using exponential models (Figure 4). Only limited differences were observed between models for 1998 (3 sites), 1999 (6 sites) and 2000 (7 sites).
    We also found that the use of growing degree days from planting in the divisor did not provide significant improvement when predicting yield compared to the use of NDVI alone. Work by Raun et al. (2000) successfully used growing degree days from the first sensing to the second sensing, but their index (EY) was bound by needing two sensor readings. Similar to results reported here, they reported that the use of growing degree days from planting to the first or second sensor reading did not improve the prediction of wheat grain yield.

DISCUSSION
    The central component behind our nitrogen fertilization optimization algorithm (NFOA) is the ability to predict potential grain yield in-season, and early enough to apply fertilizer N based on predicted need. Equally important is the ability to identify the need for fertilizer N in such a way that added N will correct for projected need.
    Because we are able to predict percent N in the grain (based on a relationship with predicted yield level), early-season plant N uptake (NDVI readings at Feekes 4 to 6) and wheat grain yield (INSEY), we propose the following procedures to determine N fertilizer application rate:

1. Predict potential grain yield (PGY) from the Grain yield-INSEY equation
PGY in (Mg ha-1) = 0.74076 + 0.10210 e577.66INSEY
2. Predict percent N in the grain based on predicted grain yield (Figure 5, total N determined on 688 samples where grain yield was recorded, 1980 to 1999)
Percent N in the grain = 0.0703PGY2 - 0.5298PGY + 3.106
3. Calculate predicted grain N uptake (predicted percent N in the grain multiplied by predicted grain yield)
4. Calculate predicted early-season plant N uptake from NDVI
Early-season plant N uptake (kg ha-1) = 14.76 + 0.7758 e5.468NDVI
5. Determine in-season topdress fertilizer N requirement = (predicted grain N uptake - predicted early-season plant N uptake)/0.70

    In our method, the predicted N deficit is the difference in predicted total grain N uptake minus the predicted early-season plant N uptake. Dividing the predicted N deficit (actual plant N need for added N) by 0.70 in step 5 basically says that we can achieve a maximum of 70% use efficiency for mid-winter applied N in winter wheat. In some regions, this should theoretically be much less where the potential for immobilization, denitrification, and/or volatilization are greater. Wuest and Cassman (1992) reported that recovery of applied N at planting ranged from 30 to 55% while that applied at flowering ranged from 55 to 80%. Raun and Johnson (1999) recently reported that worldwide nitrogen use efficiency for cereal production is approximately 33%. In this regard, the divisor could realistically range between 0.33 and 0.80.
    This procedure is different from that used by other researchers and practitioners. The proposed procedure prescribes increased N rates in areas of the field with high yield potential as indicated by INSEY and reduced N fertilizer in areas of the field with lower yield potential. In addition, this procedure accounts for the amount of N in the wheat plant (at the time of sensing) and adjusts for need accordingly.
    Field application of the process will be to compile planting date information prior to sensing, whereby NDVI readings can be collected from each 1m2, divided by the number of days from planting and a prescribed fertilizer rate applied on-the-go. Nitrogen application rates will be calculated using the previously outlined procedure, whereby the fertilizer application rate needed to optimize yield at that location will be set by the predicted yield potential. If a producer chooses to lower predicted yield potential, rates could be adjusted upward or downward, based on that input.
The use of INSEY and the Nitrogen Fertilizer Optimization Algorithm could replace N fertilization rates determined using production history (yield goals), provided that the production system allows for in-season application of fertilizer N. Application of this procedure should result in increased grain yields at lower N rates when INSEY is computed and applied to each 1m2. This procedure should also increase N use efficiency (decreased N applied where early-season plant N uptake was already high) when the production system allows for in-season application of fertilizer N.

References

Fiez, T.E., W.L. Pan, and B.C. Miller. 1995. Nitrogen use efficiency of winter wheat among landscape positions. Soil Sci. Soc. Amer. J. 59:1666-1671.

Filella, I., L. Serrano, J. Serra and J. Penuelas. 1995. Evaluating wheat nitrogen status with canopy reflectance indices and discriminant analysis. Crop Sci. 35:1400-1405.

Halvorson, A.D., C.A. Reule, and R.F. Follett. 1999. Nitrogen fertilization effects on soil carbon and nitrogen in a dryland cropping system. Soil Sci. Soc. Amer. J. 63:912-917.

Raun, W.R., and G.V. Johnson. 1999. Improving nitrogen use efficiency for cereal production. Agron. J. 91:357-363.

Raun, W.R., J.B. Solie, G.V. Johnson, M.L. Stone, E.V. Lukina, W.E. Thomason, and J.S. Schepers. 2000. In-season prediction of potential grain yield in winter wheat using canopy reflectance. Agron. J. (in press).

Schepers, J.S., D.D. Francis, and M.T. Thompson. 1989. Simultaneous determination of total C, total N and 15N on soil and plant material. Commun. Soil Sci. Plant Anal. 20:949-959.

Sembiring, H., H.L. Lees, W.R. Raun, G.V. Johnson, J.B. Solie, M.L. Stone, M.J. DeLeon, E.V. Lukina, D.A. Cossey, J.M. LaRuffa, C.W. Woolfolk, S.B. Phillips, and W.E. Thomason, . 2000. Effect of growth stage and variety on spectral radiance in winter wheat. J. Plant Nutr. 23:141-149.

Solie, J.B., W.R. Raun and M.L. Stone. 1999. Submeter spatial variability of selected soil and bermudagrass production variables. Soil Sci. Soc. Am. J. 63:1724-1733.

Sowers, K.E., B.C. Miller and W.L. Pan. 1994. Optimizing yield and grain protein in soft white winter wheat with split nitrogen applications. Agron. J. 86:1020-1025.

Thomason, W.E., W.R. Raun and G.V. Johnson. 2000. Winter wheat fertilizer nitrogen use efficiency in grain and forage production systems. J. Plant Nutr. (in press).

Tilman, D. 1999. Global environmental impacts of agricultural expansion: the need for sustainable and efficient practices. Proc. National Academy of Sciences of the United States of America. 96(11):5995-6000.

Wuest, S.B., and K.G. Cassman. 1992. Fertilizer-nitrogen use efficiency of irrigated wheat: I. Uptake efficiency of preplant versus late-season application. Agron. J. 84:682-688.

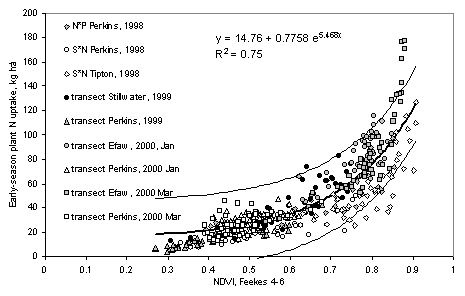
FIGURE 1.  Relationship between the normalized difference vegetation index computed from red and near infrared reflectance readings from winter wheat at Feekes physiological stages 4 to 6 and measured early-season plant N uptake from nine experiments, 1998-2000. 

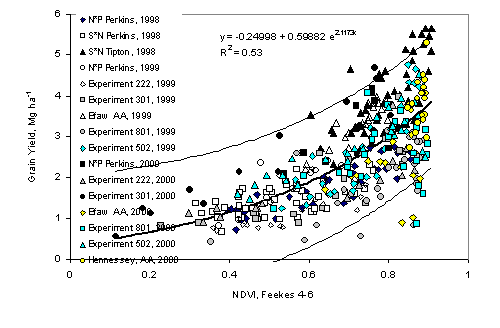
FIGURE 2.  Relationship between the normalized difference vegetation index computed from red and near infrared reflectance readings from winter wheat at Feekes physiological stages 4 to 6 and measured grain yield from sixteen experiments, 1998-2000. 

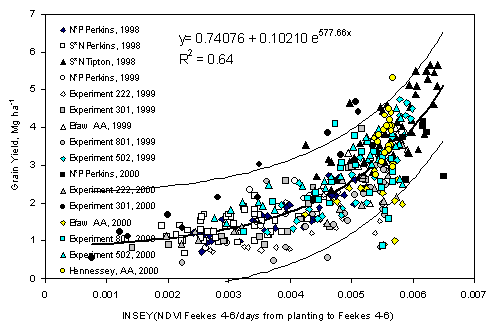
FIGURE 3.  Relationship between in season estimated grain yield (INSEY) computed from NDVI readings collected between Feekes physiological growth stages 4 to 6, divided by the number of days from planting to the reading date, and measured grain yield from sixteen winter wheat experiments, 1998-2000. 

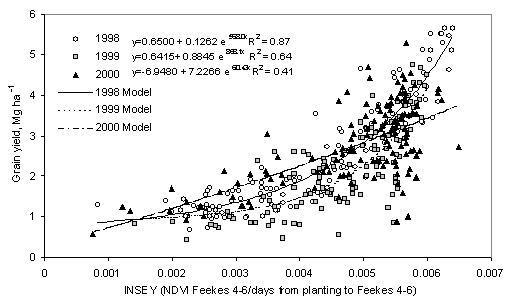
FIGURE 4.  Relationship between in season estimated grain yield (INSEY) computed from NDVI readings collected between Feekes physiological growth stages 4 to 6, divided by the number of days from planting to the reading date, and measured grain yield (by year) from sixteen experiments, 1998-2000. 

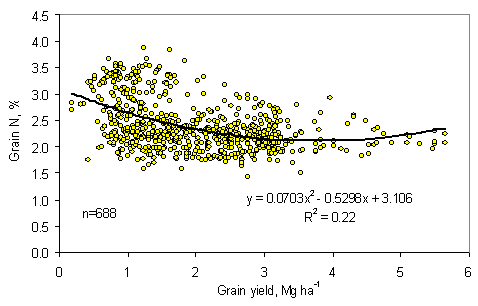
FIGURE 5.  Relationship between total N in wheat grain (%) and grain yield, from multiple experiments conducted from 1980 to 2000.

TABLE 1.  Nine experiments where forage N uptake, and sensor readings were collected, number of plots,
physiological growth stage, variety, and sensor/sampling date.  

§S*N, row spacing by N rate experiment
¶N*P, N rate by P rate experiment

TABLE 2.  Sixteen experiments where sensor and winter wheat grain yield data were collected,
planting and harvest date, and days from planting to sensing, 1998-2000.

§S*N, row spacing by N rate experiment
¶N*P, N rate by P rate experiment

Return to the