Covariance and Autocorrelation

Proc Corr;

data one;
input red nir NDVI yield height;
cards;
.5 .6 .7 4000 32
.4 .7 .8 5000 39
.5 .8 .9 5500 41
.4 .5 .7 3500 30
.3 .5 .6 3400 29
.2 .4 .5 2200 25
.24 .45 .55 2400 28
.29 .46 .58 2600 29
proc corr;
  var red nir NDVI yield height;
  run;
proc corr;
  var red nir;
  with yield;
run;

"Autocorrelation"  if red is correlated with NDVI, what does this mean?

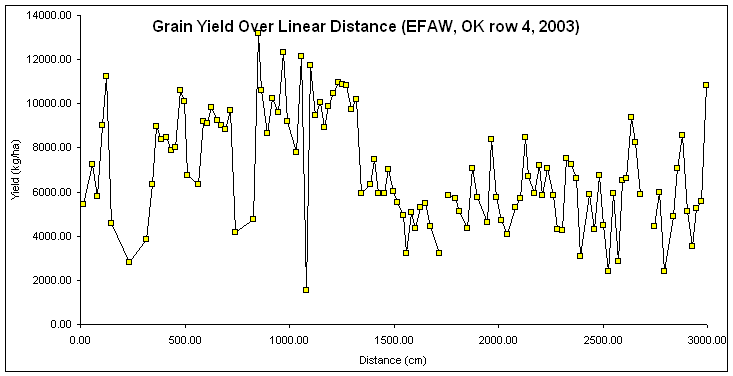
Is this "Autocorrelation" plotting yield as a function of distance, since distance (x) was used to compute yield (y)?

Covariance (go to RCBD example, #222, use GN as a covariate)

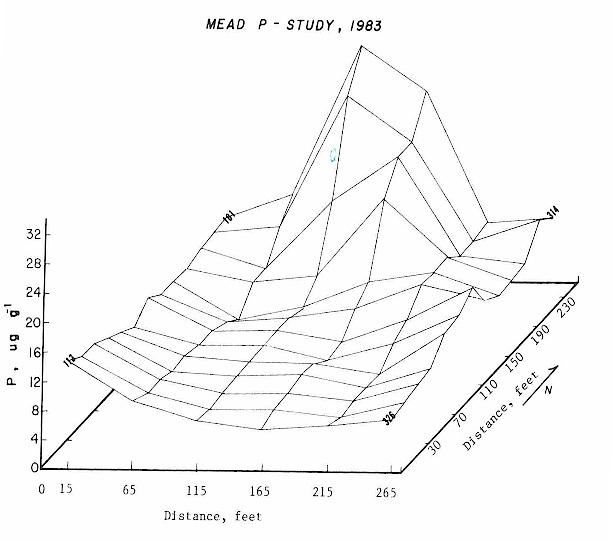
Rule: Run anova using preplant P as a dependent variable.  Treatment cannot be significant.
Requires Planning!

data one;
input rep nrate tillage yield preP;
cards;
1 0 0 20 16
1 50 0 25 13
1 100 0 29 13
1 150 0 35 14
1 0 1 35 18
1 50 1 35 16
1 100 1 38 11
1 150 1 39 19
2 0 0 20 22
2 50 0 26 23
2 100 0 30 21
2 150 0 32 25
2 0 1 36 19
2 50 1 36 11
2 100 1 37 18
2 150 1 40 16
3 0 0 17 28
3 50 0 22 19
3 100 0 25 28
3 150 0 29 22
3 0 1 29 23
3 50 1 34 25
3 100 1 38 24
3 150 1 40 18
proc print;
proc glm;
classes tillage nrate;
model yield = nrate tillage nrate*tillage preP;
lsmeans nrate tillage nrate*tillage;
run;